FIND THE AREA AND PERIMETER OF THE GIVEN FIGURE

Find the area and perimeter of the following figures.

Example 1 :

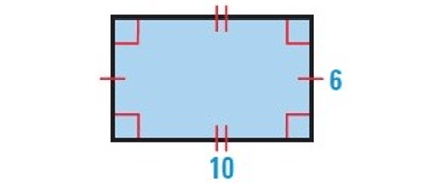
Solution :

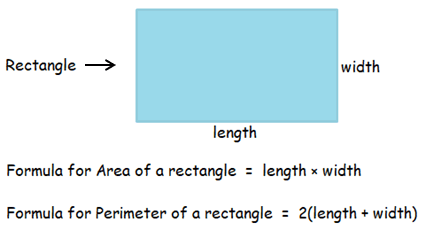
By observing the figure, it is a rectangle.

Finding the area :

Area of a rectangle  =  length × width

Here length  =  10, width  =  6

=  10 × 6

Area  =  60 sq.units

Finding the perimeter :

Perimeter of a rectangle  =  2(length + width)

=  2(10 + 6)

=  2(16)

Perimeter  =  32 units

Example 2 :

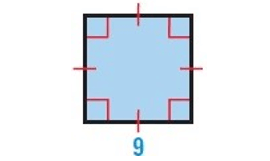
Solution :

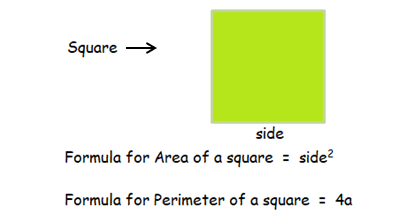
By observing the figure, it is a square.

Finding the area :

Area of a square  =  side²

Here side(a)  =  9

=  9²

Area  =  81 sq.units

Finding the perimeter :

Perimeter of a square  =  4a

=  4(9)

Perimeter  =  36 units

Example 3 :

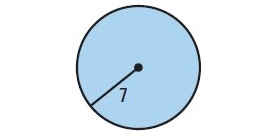
Solution :

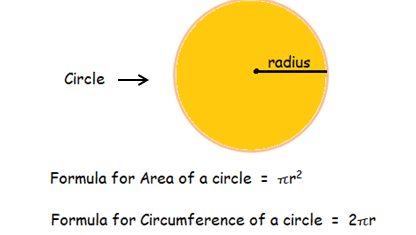
By observing the figure, it is a circle.

Finding the area :

Area of a circle  =  πr²

Here radius  =  7

=  π7²

=  49π

Area  =  49π sq.units

Finding the circumference :

Circumference of a circle  =  2πr

=  2π(7)

Circumference  =  14π units

Example 4 :

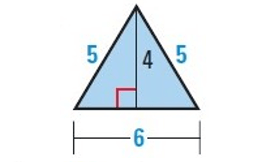
Solution :

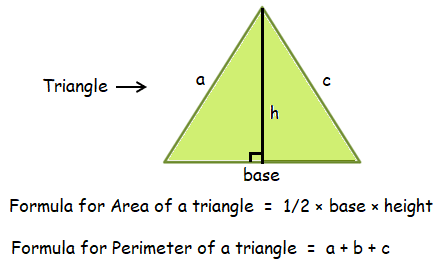
By observing the figure, it is a triangle.

Finding the area :

Area of a triangle  =  1/2 × base × height

Here base  =  6, height  =  4

=  1/2 × 6 × 4

Area  =  12 sq.units

Finding the perimeter :

Perimeter of a triangle  =  a + b + c

Here side(a)  =  5, base(b)  =  6 and side(c)  =  5

=  5 + 6 + 5

Perimeter  =  16 units

Example 5 :

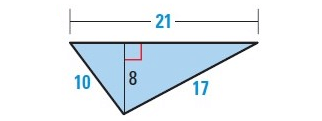
Solution :

By observing the figure, it is a triangle.

Finding the area :

Area of a triangle  =  1/2 × base × height

Here base  =  21, height  =  8

=  1/2 × 21 × 8

Area  =  84 sq.units

Finding the perimeter :

Perimeter of a triangle  =  a + b + c

Here side(a)  =  10, base(b)  =  21 and side(c)  =  17

=  10 + 21 + 17

Perimeter  =  48 units

Example 6 :

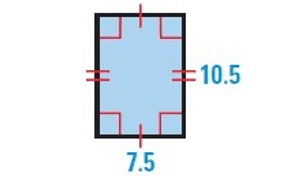
Solution :

By observing the figure, it is a rectangle.

Finding the area :

Area of a rectangle  =  length × width

Here length  =  10.5 and width  =  7.5

=  10.5 × 7.5

Area  =  78.75 sq.units

Finding the perimeter :

Perimeter of a rectangle  =  2(length + width)

=  2(10.5 + 7.5)

=  2(18)

Perimeter  =  36 units

Example 7 :

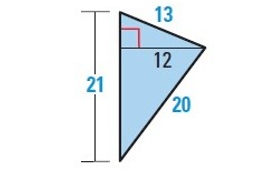
Solution :

By observing the figure, it is a triangle.

Finding the area :

Area of a triangle  =  1/2 × base × height

Here base  =  21, height  =  12

=  1/2 × 21 × 12

Area  =  126 sq.units

Finding the perimeter :

Perimeter of a triangle  =  a + b + c

Here side(a)  =  13, base(b)  =  21 and side(c)  =  20

=  13 + 21 + 20

Perimeter  =  54 units

Example 8 :

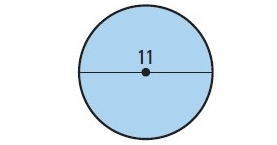
Solution :

By observing the figure, it is a circle.

Finding the area :

Area of a circle  =  πr²

Here diameter  =  11

So, radius  =  d/2  =  11/2

r  =  5.5

=  π(5.5)²

=  30.25π

Area  =  30.25π sq.units

Finding the circumference :

Circumference of a circle  =  2πr

=  2π(5.5)

Circumference  =  11π units

Example 9 :

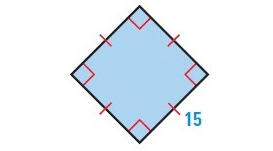
Solution :

By observing the figure, it is a square.

Finding the area :

Area of a square  =  side²

Here side(a)  =  15

=  15²

Area  =  225 sq.units

Finding the perimeter :

Perimeter of a square  =  4a

=  4(15)

Perimeter  =  60 units

Example 10 :

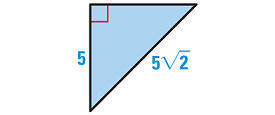
Solution :

Because we want to find the area of the triangle, we have to know its base and height.

To know the base and height of the triangle, let us rotate the given triangle as shown below. 

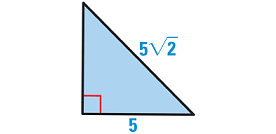
Use Pythagorean theorem to find the height of the triangle.

h²+ 5²  =  (5√2)²

h² + 25  =  5² ⋅ (√2)²

h² + 25  =  25⋅2

h² + 25  =  50

Subtract 25 from each side. 

h²  =  25

h²  =  5²

h  =  5

Finding the area :

Area of the triangle =  (1/2) ⋅ base ⋅ height

=  (1/2) ⋅ 5 ⋅ 5

=  12.5 square units

Finding the perimeter :

Perimeter of the triangle :

=  Sum of the lengths of all the three sides

=  5 + 5 + 5√2

=  (10 + 5√2) units

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.