FIND THE APPROXIMATE VALUE USING LINEAR APPROXIMATION

Let f : (a,b)→R be a differentiable function and

x₀ ∈ (a, b)

We define the linear approximation L of f at x₀ by

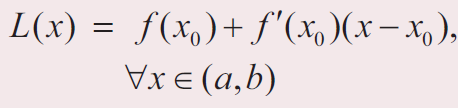
Problem 1 :

Let f (x)  =  ∛x . Find the linear approximation at x = 27. Use the linear approximation to approximate ∛27.2

L(x)  =  f(x₀) + f'(x₀) (x-x₀)

Solution :

f(x)  =  ∛x

Let x₀  =  27 and x  =  27.2

L(x)  =  f(x₀) + f'(x₀) (x - x₀)

L(27.2)  =  3 + (1/27) (27.2-27)

L(27.2)  =  3 + (1/27) (0.2)

L(27.2)  =  3 + 0.0074

L(27.2)  =  3.0074 (approximately)

Problem 2 :

Use the linear approximation to find approximate values of

(i)  (123)^2/3

Solution :

f(x)  =  (x)^2/3

Let x  =  123 and x₀  =  125 (the nearest whole number)

L(x)  =  f(x₀) + f'(x₀) (x - x₀)

L(123)  =  25 + (2/15) (123-125)

L(123)  =  25 + (2/15) (-2)

L(123)  =  25 - (4/15)

L(123)  =  25 - 0.2667

L(123)  =  24.733

So, the approximate value of (123)^2/3 is 24.733.

(ii)  (15)^1/4

Solution :

L(x)  =  f(x₀) + f'(x₀)(x-x₀)

Let x₀  =  16 and x  =  15

L(15)  =  f(16) + f'(16)(x-x₀)  ----(1)

L(15)  =  f(16) + f'(16)(x-x₀)  ----(1)

By applying the values in (1), we get

L(15)  =  2 + (1/32)(15-16)

L(15)  =  2 + (1/32)(-1)

L(15)  =  2 - 0.03125

L(15)  =  1.968 (approximately)

So, the approximate value of (15)^1/4 is  1.968.

(iii)  ∛26

Solution :

Let f(x)  =   ∛x

Let x  =  26 and x₀  =  27

L(x)  =  f(x₀) + f'(x₀) (x-x₀)

L(26)  =  f(27) + f'(27) (x-x₀)  ----(1)

By applying these value in (1), we get

L(26)  =  3 + (1/27) (27-26)

L(26)  =  3 + (1/27) (1)

L(26)  =  3 + 0.0370

L(26)  =  3.0370

So, the approximate value of ∛26 is 3.0370.

Problem 3 :

Consider the implicit function defined by 3(x² + y²)² = 100xy . Use a tangent line approximation at the point (3,1) to estimate the value of y when x = 3.1.

Solution :

Even though y is defined implicitly as a function of x here, the tangent line to the graph of 3(x² + y²)² = 100xy at (3, 1) can easily be found and used to estimate y for x near 3.

First, find y. Differentiating both sides of 3(x² + y2)2 = 100xy with respect to x gives

6(x² + y²)(2x + 2 yy') = 100y + 100xy'

Now substitute (x, y) = (3, 1)

6(9 + 1)(6 + 2y') = 100 + 300 y'

60(6 + 2y') = 100 + 300 y'

360 + 120y'= 100 + 300y'

360 - 100 = 300y'- 120y'

260 = 180y'

y' = 260 / 180

y' = 13/9

which yields y' = 13/9. Thus the equation of the tangent line is

y − 1 = (13/9) (x−3)

y - 1 = (13x/9) - (13/3)

y = (13x/9) - (13/3) + 1

y = (13x/9) + (-13 + 3)/3

y = (13x/9) - (10/3)

Thus, for points (x,y) on the graph of 3(x² + y²)² = 100xy with x near 3,

y ≈ (13x/9) − (30/9) 

Setting x = 3.1 in this last equation gives

y ≈ 103/90 

= 1.14 to two decimals.

Problem 4 :

Finding a local linear approximation at a given point is finding the equation of the tangent line at that point.

a) Find the local linear approximation of f(x) = x³ - 2x + 3 at the point where x = 2.

b) Use your approximation to estimate f(2.1), f(1.9) and f(1.99).

Solution :

f(x) = x³ - 2x + 3

Let x₀  = 2

f'(x) = 3x² - 2(1) + 0

f'(x) = 3x² - 2

f'(x₀) = 3(2)² - 2

= 12 - 2

f'(x₀) = 10

L(x)  =  f(x₀) + f'(x₀) (x-x₀)

L(2)  =  f(2) + f'(2) (x-2)

Finding the value of f(2),

f(2) = 2³ - 2(2) + 3

= 8 - 4 + 3

= 7

L(2) = 7 + 10 (x - 2)

= 7 + 10x - 20

L(2) = 10x - 13

Using the result above, finding the linear approximation for f(2.1), f(1.9) and f(1.99).

L(2.1) = 10(2.1) - 13

= 21 - 13

= 8

L(1.9) = 10(1.9) - 13

= 19 - 13

= 6

L(1.99) = 10(1.99) - 13

= 19.9 - 13

= 6.9

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.