FIND SUM OF NATURAL NUMBERS BETWEEN TWO NUMBERS

Question 1 :

Find the sum of all natural numbers between 300 and 500 which are divisible by 11.

Solution :

To find the first number greater than 300 and divisible by 11, we use the following shortcut.

308 + 319 + 330 +........

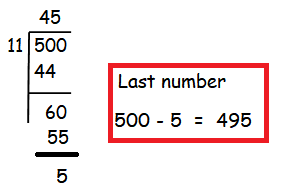
308 + 319 + 330 +........+495

s_n  =  (n/2)[a+l]

n  =  [(l-a)/d]+1

n  =  [(495-308)/11]+1

n  =  (187/11)+1

n  =  17+1

n  =  18

s₁₈  =  (18/2)[308+495]

s₁₈  =  9(803)

s₁₈  =  7227

Question 2 :

Find the  sum of all natural numbers between 100  and 200 which are not divisible by 5.

Solution :

Sum of natural numbers between 100 and 200 which are not divisible by 5.

  =  Sum of natural number from 100 to 200 - Sum of natural numbers which is divisible by 5 between 100 to 200.

=  (100+101+...........+200)-(100+105+110+....+200)

Number of terms in the series 

100+101+...........+200

n  =  [(200-100)/1] + 1

n  =  101

Number of terms in the series 

100+105+110+....+200

n  =  [(200-100)/5] + 1

n  =  21

Sum of series 100+101+...........+200

=  (101/2) (100+200) 

=  101(150)

=  15150

Sum of series 100+105+110+....+200

=  (21/2) (100+200) 

=  21(150)

=  3150

The required sum is  =  15150 - 3150

=  12000

So, the sum of natural numbers 12000.

Question 3 :

Solve 1 + 6 + 11 + 16 + ..........  + x = 148

Solution :

1 + 6 + 11 + 16 + ..........  + x = 148

n  =  [(l-a)/d] + 1

n  =  [(x-1)/5] + 1

n  =  (x+4)/5

s_n  =  (n/2)[a+l]

148  =  ((x+4)/10)(1+x)

1480  =  x²+ 5x+4

x²+ 5x+4-1480  =  0

x²+ 5x-1476  =  0

(x+41)(x-36)  =  0

x  =  36

So, the last term is 36.

Question 4 :

Divide 144 into three parts which are in arithmetic progression and such that the largest is twice the smallest, the smallest of three numbers will be :

a)  48   b b)  36    c)  13     d)  32

Solution :

Let three numbers in arithmetic progression will be 

a - d, a and a + d

Here the smallest = a - d and largest = a + d

a + d = 2(a - d) ----(1)

Sum of three terms = 144

a - d + a + a + d = 144

3a = 144

a = 144/3

a = 48

Appling the value of a in (1), we get

48 + d = 2(48 - d)

48 + d = 96 - 2d

48 - 96 = -2d - d

-48 = -3d

d = 48/3

d = 16

Smallest number = a - d

= 48 - 16

= 32

Question 5 :

If the sum of 3 arithmetic means between a and 22 is 42, then a = ?

Solution :

Let three arithmetic mean between a and 22 are a₂, a₃ and a₄.

From the above arrangement, we know that the first term is a and 5th term is 22.

a₅ = a + 4d = 22 -----(1)

Arithmetic mean of a2, a3 and a4 = 42

a + d + a + 2d + a + 3d = 42

3a + 6d = 42

Dividing by 3, we get 

a + 2d = 14 ------(2)

(1) - (2)

a + 4d - a - 2d = 22 - 14

2d = 8

d = 4

Applying the value of d in (1), we get

a + 4(2) = 22

a + 8 = 22

a = 22 - 8

a = 14

So, the first term is 14.

Question 6 :

If 8^th term of an arithmetic progression is 15, then sum of its 15 terms.

a)  15     b)  0    c)  225     d)  225/2

Solution :

8^th term = 15

a + 7d = 15

Finding sum of 15 terms :

= (n/2) [2a + (n - 1) d]

= (15/2)[2a + (15 - 1)d]

= (15/2)[2a + 14d]

= (15/2) x 2(a + 7d)

= 15 (15)

= 225

So, the required sum is 225.

Question 7 :

If the sum of the 4^th term and the 12^th term of an arithmetic progression is 8, what is the sum of 15 terms of the progression ?

a)  60     b)  120      c)  110        d)  150

Solution :

4^th term + 12^th term = 8

a + 3d + a + 11d = 8

2a + 14d = 8

Dividing by 2, we get

a + 7d = 4 ----(1)

Finding sum of 15 terms :

= (n/2) [2a + (n - 1) d]

= (15/2)[2a + (15 - 1)d]

= (15/2)[2a + 14d]

= (15/2) x 2(a + 7d)

= 15 (4)

= 60

So, the required sum is 60.

Question 8 :

An arithmetic progression has 13 terms whose sum is 143. The third term is 5 so the first term is 

a)  4     b)  7      c)  9         d)  2

Solution :

S₁₃ = 143

a₃ = 5

a + 2d = 5 ----(1)

S_n = (n/2) [a + l]

(13/2)[a + l] = 143

(13/2)[2a + (13 - 1)d] = 143

(13/2)[2a + 12d] = 143

(13/2) x 2 [a + 6d] = 143

13(a + 6d) = 143

a + 6d = 143/13

a + 6d = 11 ----(2)

(1) - (2)

2d - 6d = 5 - 11

-4d = -6

d = 3/2

Applying the value of d, we get

a + 2(3/2) = 5

a + 3 = 5

a = 5 - 3

a = 2

So, the first term is 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.