FIND RANGE OF FUNCTION FOR GIVEN DOMAIN

Domain :

The domain of a function f(x) is the set of all values for which the function is defined

Range :

The range of the function is the set of all values that f takes.

They may also have been called the input and output of the function.) .

It is like evaluating functions for the given value of x.

Example 1 :

Consider f(x)  =  x² for the domain {-2, -1, 0, 1, 2}

Find the range.

Solution :

Given, f(x)  =  x²

Range  =  {4, 1, 0, 1, 4}

Example 2 :

For the following functions of

f : x -> f(x) on -2≤x≤2

where x ∈ z

(a)  List the elements of the domain of f(x) using set notation.

(b)  List the elements of the range of f(x) using set notation.

(1)  f(x)  =  1/(x+3)   

(2)  (x+3)/x  and x ≠ 0

 (3)  f(x)  =  3^x

(1)  Solution :

Given :

f(x)  =  1/(x+3)

Domain  =  {-2, -1, 0, 1, 2}

Range  =  {1, 1/2, 1/3, 1/4, 1/5}

(2)  Solution :

Given :

f(x)  =  (x+3)/x

Domain  =  {-2, -1, 0, 1, 2}

Range  =  {-1/2, -2, 5/2, 4}

(3)  Solution :

Given :

f(x)  =  3^x

Domain  =  {-2, -1, 0, 1, 2}

Range  =  {1/9, 1/3, 1, 3, 9}

Example 3 :

Find the range of f (x) = −x + 4 for the

domain {–3, –2, –1, 1}

Solution :

To find range of the given function from the given domain, we have to apply the given values one by one in the given function.

f(x) = −x + 4

So, the range is {7, 6, 5, 3}.

Example 4 :

To rent a bike, Max pays a at rate plus an hourly rental fee. The graph shows the amount, c dollars, he pays based on the number of hours, t, he uses the bike. Use the graph to answer the following question:

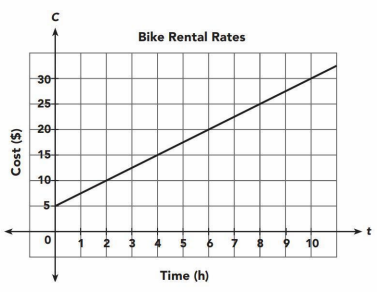
What is the domain and range of the function?

Solution :

Domain of the function 0 ≤ h < ∞

Range is 5 ≤ c < ∞

Example 5 :

A car rental company charges $10 an hour (a part of an hour rounds up to the next hour) to rent a car. The limit to the number of hours you can rent the car is 8 hours.

a. Write a rule in function notation for this situation.

b. What is a reasonable domain and range for this situation?

c) The graph will be discrete or continuous.

Solution :

a) Let x be the number of hours of renting car.

Let f(x) be the cost paid for renting car.

Cost of renting 1 hour = $10

The required function will be,

f(x) = 10x

b. The minimum number of hours of renting car is 0 and maximum number of hours of renting car. Number of hours rented should be whole number.

So, domain is {0, 1, 2, 3, 4, 5, 6, 7, 8}

When h = 0, f(0) = 0

When h = 1, f(1) = 10

When h = 2, f(2) = 20

and so on

So, range is {0, 10, 20, 30, 40, 50, 60, 70, 80}

c) The graph should be discrete, because we can pay every hours and it should be whole numbers not a decimal.

Example 5 :

The American Sycamore tree grows approximately 6 feet per year until they reach a maximum height of 66 ft.

a. Write a rule in function notation for this situation.

b. What is a reasonable domain and range for this situation?

c) The graph will be discrete or continuous.

Solution :

a) Let x be the number of years.

Let f(x) be the height of the tree.

a) The required function will be,

f(x) = 6x

When f(x) = 66

66 = 6x

x = 66/6

x = 11

b)  Domain = 0 ≤ x ≤ 11

Range = 0 ≤ f(x) ≤ 66

c) The graph must be continuous, because the growth will not stop at only integers.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.