FIND QUOTIENT AND REMAINDER USING SYNTHETIC DIVISION

Find the quotient and remainder for the following using synthetic division:

Question 1 :

(x³ + x² - 7x - 3) ÷ (x - 3)

Solution :

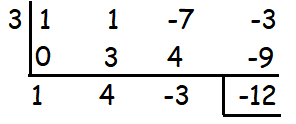
Quotient  =  x² + 4x - 3

Remainder  =  -12

Question 2 :

(x³ + 2x² - x - 4) ÷ (x + 2)

Solution :

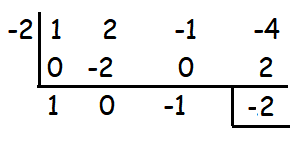
Quotient  =  x² + 0x - 1

Remainder  =  -2

Question 3 :

(3x³ - 2x² + 7x - 5) ÷ (x + 3)

Solution :

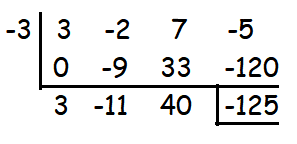
Quotient  =  3x² - 11x + 40

Remainder  =  -125

Question 4 :

(8x⁴ - 2x² + 6x + 5) ÷ (4x + 1)

Solution :

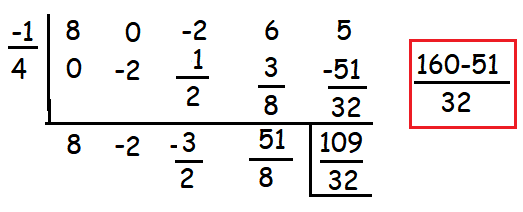
Quotient : 8x³ - 2x² -(3x/2) + (51/8)

Remainder  : 109/32

Question 5 :

If the quotient obtained on dividing (8x⁴ - 2x² + 6x - 7) by (2x + 1) is (4x³ + px² - qx + 3) then find p, q and also the remainder.

Solution :

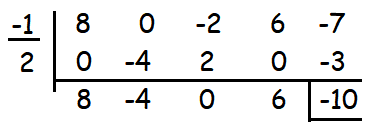
8x³ - 4x2 + 0x + 6 

Dividing the quotient by 2, we get 

4x³ - 2x² + 0x + 3 

The value of p and q are -2 and 0 respectively and remainder is -10.

Question 6 :

If the quotient obtained on dividing 3x³ + 11x² + 34x + 106 by x - 3 is 3x² + ax + b, then find a, b and also the remainder.

Solution :

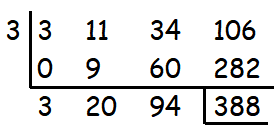
Quotient  =  3x² + 20x + 94

Given quotient  =  3x² + ax + b

By comparing the corresponding terms, we get

3x² + 20x + 94  =  3x² + ax + b

a = 20 and b = 94.

So, the values of a and b are 20 and 94 respectively.

Question 7 :

If f(x) = 3x³ + 4x² - 5x + 7, find f(-4) using

a) Synthetic division

b) The remainder theorem.

Solution :

f(x) = 3x³ + 4x² - 5x + 7

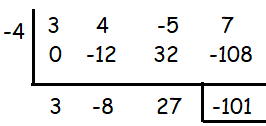
Using synthetic division shown above,

Quotient = 3x² - 8x + 27

Remainder = -101

b) Using remainder theorem,

To find the value of f(-4), weh ave to apply -4 in place of x.

f(-4) = 3(-4)³ + 4(-4)² - 5(-4) + 7

= 3(-64) + 4(16) + 20 + 7

= -192 + 64 + 27

= -192 + 91

= -101

Remainder = -101

In both ways we must get the same result.

Question 8 :

Solve the equation 2x³ - 3x² - 11x + 6 = 0 given that -2 is a zero of f(x) = 2x³ - 3x² - 11x + 6

Solution :

Given that -2 is a zero of the polynomial f(x) = 2x³ - 3x² - 11x + 6

Then, applying x = -2 we get 0 as remainder.

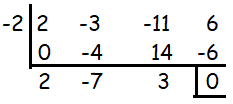
From the above steps, it is clear that -2 is one of the zeroes, to find the other zeroes we have to equate the quotient to 0.

2x² - 7x + 3 = 0

2x² - 6x - 1x + 3 = 0

2x(x - 3) - 1(x - 3) = 0

(2x - 1)(x - 3) = 0

Eqauting each factor to 0, we get

2x - 1 = 0 and x - 3 = 0

2x = 1 and x = 3

x = 1/2

So, the solutions are -2, 1/2 and 3.

Question 9 :

Use synthetic division to divide f(x) = x³ - 4x² + x + 6 by x + 1. Use the result to find all zeroes of f.

Solution :

Given that,

f(x) = x³ - 4x² + x + 6

We have to divide this polynomial by x + 1, to use synthetic division we solve for x by x + 1 = 0

x = -1

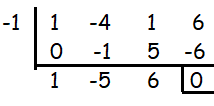
By dividing the given polynomial by x + 1, we get the remainder as 0. So, -1 is one of the zeroes of the polynomial.

Quotient = x² - 5x + 6

To solve this, we will equate this to 0.

x² - 5x + 6 = 0

x² - 2x - 3x + 6 = 0

x(x - 2) - 3(x - 2) = 0

(x - 3)(x - 2) = 0

x - 3 and x - 2 = 0

x = 3 and x = 2

So, the solutions are -1, 2 and 3.

Question 10 :

Solve the equation 2x³ - 5x² + x + 2 given that 2 is a zero of f(x) = 2x³ - 5x² + x + 2.

Solution :

Given that,

f(x) = 2x³ - 5x² + x + 2

Since 2 is a zero of the polynomial, by dividing this polynomial by x - 2, we get 0 as remainder.

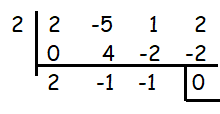
Quotient = 2x² - 1x - 1

Remainder = 0

From this 2 is one of the zeroes of the polnomial, to get the other zeroes, we equate the quadratic to 0.

2x² - 1x - 1 = 0

2x² - 2x + 1x - 1 = 0

2x(x - 1) + 1(x - 1) = 0

(2x + 1)(x - 1) = 0

2x + 1 = 0 and x - 1 = 0

2x = -1 and x = 1

x = -1/2 and x = 1

So, the required zeroes are -1/2, 1 and 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.