FIND PROBABILITY OF AN EVENT EXAMPLES

Example 1 :

A company manufactures 10000 Laptops in 6 months. Out of which 25 of them are found to be defective. When you choose one Laptop from the manufactured, what is the probability that selected Laptop is a good one.

Solution : 

Number of laptops  n(S)  =  10000

Number of defective lap top  =  25

Let "A" be the event of choosing good laptop.

Number of good laptop  =  10000 - 25

n(A)  =  9975

p(A)  =  n(A)/n(S)

p(A)  =  9975/10000

p(A)  =  0.9975

Example 2 :

In a survey of 400 youngsters aged 16-20 years, it was found that 191 have their voter ID card. If a youngster is selected at random, find the probability that the youngster does not have their voter ID card.

Solution :

Total number of youngster  n(S)  =  400

Let "A" be the event of choosing youngster does not have ID card

  =  400 - 191

n(A)  =  209

P(A)  =  n(A)/n(S)

P(A)  =  209/400

Example 3 :

The probability of guessing the correct answer to a certain question is x/3 . If the probability of not guessing the correct answer is x/5, then find the value of x.

Solution :

P(A) = Probability of getting correct answer

p(B)  =  Probability of getting not guessing correct answer

P(A) + p(B)  =  1

(x/3) + (x/5)  =  1

(5x + 3x)/15  =  1

8x  =  15

x  =  15/8

Example 4 :

If a probability of a player winning a particular tennis match is 0.72. What is the probability of the player loosing the match?

Solution :

Let "A" be event of winning a game. A bar be the event of lossing the game.

p(A) + p(A bar)  =  1

0.72  + p(A bar)  =  1

p(A bar)  =  1 - 0.72

p(A bar)  =  0.28

Example 5 :

1500 families were surveyed and following data was recorded about their maids at homes

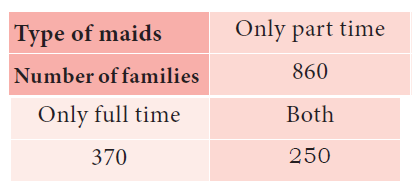
A family is selected at random. Find the probability that the family selected has (i) Both types of maids (ii) Part time maids (iii) No maids

Solution :

Total number of families n(S)  =  1500

Let "A" be the event of selecting maid of both types.

n(A)  =  250

p(A)  =  n(A)/n(S)

p(A)  =  250/1500

p(A)  =  1/6

(ii) Part time maids

Let "B" be the event of selecting maid of part time

n(B)  =  8600

p(B)  =  n(B)/n(S) 

p(B)  =  860/1500

p(B)  =  43/75

(iii) No maids

Number of families selected maid  =  860 + 370 + 250

  =  1480

n(C)  =  1500 - 1480

n(C)  =  20

P(C)  =  n(C)/n(S)

  =  20/1500

p(C)  =  1/75   

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.