FIND MEAN MEDIAN AND MODE OF GROUPED DATA

Mean :

Arithmetic mean (AM) is one of the measures of central tendency which can be defined as the sum of all observations divided by the number of observations. 

Median :

Median is defined as the middle value of the data when the data is arranged in ascending or descending order.

Mode :

If a set of individual observations are given, then the mode is the value which occurs most often.

Let us look into some example problems to understand how to find mean, median and mode of the grouped data.

Example 1 :

Find the mean, median and mode for the following frequency table:

Solution :

Arithmetic mean  =  ∑fx / N  

Arithmetic mean  =  ∑fx / N  =  1680 / 60

  =  28

Hence the required arithmetic mean for the given data is 28.

Median :

Here, the total frequency, N = ∑f = 60

N/2  =  60 / 2  =  30

The median is (N/2)^th value = 30^th value.

Now, 30^th value occurs in the cumulative frequency 31, whose corresponding x value is 25.

Hence, the median = 25.

Mode :

By observing the given data set, the number 30 occurs more number of times. That is 15 times.

Hence the mode is 30.

Mean  =  28

Mode  =  25 and

Mode  =  30.

Example 2 :

Find the mean, median and mode for the following frequency table:

Solution :

To find arithmetic mean for this problem, let us use assumed mean method.

Here A  =  25

Arithmetic mean  =  A + [∑fd / N] 

  =  25 + (0/112)

  =  25 + 0

=  25

Hence the required arithmetic mean for the given data is 25.

Median :

Here, the total frequency, N = ∑f = 112

N/2  =  112 / 2  =  61

The median is (N/2)^th value = 61^th value.

Now, 61^th value occurs in the cumulative frequency 25, whose corresponding x value is 25.

Hence, the median = 25.

Mode :

By observing the given data set, the number 23 occurs more number of times. That is 20 times.

Hence the mode is 23.

Mean  =  25

Mode  =  25

Mode  =  23

Example 3 :

For this column graph on shoe sizes, determine the 

(i) Mode

(ii) Median shoe size

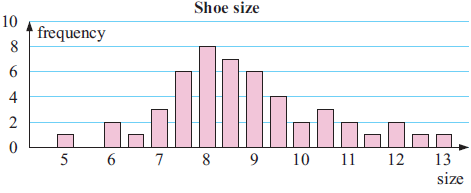
Solution :

a) Mode is the most repeating value. By observing the column graph, 8 is the most repeating value. Then 8 is the mode.

b)  Median

N = 50 (even)

N/2 = 50/2

= 25^th value

Median = 8.5

Example 4 :

The mean of 12 scores is 8.8. What is the sum of the scores?

Solution :

Number of scores = 12

Mean = 8.8

Mean = Total scores / Number of terms

8.8 = Total scores / 12

Total scores = 8.8(12)

= 105.6

Example 5 :

While on camping holiday, Daffyd drove on average 325 km per day for a period of 7 days. How far Daffyd  drive in total while on holiday ?

Solution :

Average = 325

Total number of days = 7

Average distance covered = total distance / total number of days

325 = total distance / 7

Total distance = 325(7)

= 2275

Example 6 :

Find a, given that 10, a, 15, 20, a, a, 17, 7 and 15 have a mean 12.

Solution :

Mean = 12

Total number of terms = 9

(10 + a + 15 + 20 + a + a + 17 + 7 + 15)/9 = 12

(3a + 84)/9 = 12

3a + 84 = 12(9)

3a + 84 = 108

3a = 108 - 84

3a = 24

a = 24/3

a = 8

So, the value of a is 8.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.