FIND fxy and fyx USING PARTIAL DERIVATIVE OF A FUNCTION

For each of the following functions find the f_x and f_y and show that f_xy  =  f_yx

Problem 1 :

f (x, y)  =  3x/(y+sinx)

Solution :

f (x, y)  =  3x/(y+sinx)

Finding f_x :

Differentiate with respect to x. Treat y as constant.

u  =  3x and v  =  y+sinx

u'  =  3 and v'  =  0+cosx  ==>  cosx

f_x  =  [(y+sinx)(3) - 3x(cosx)]/(y+sinx)²

f_x  =  [3y+3sinx - 3xcosx]/(y+sinx)²

Finding f_xy :

Differentiate with respect to y. Treat x as constant.

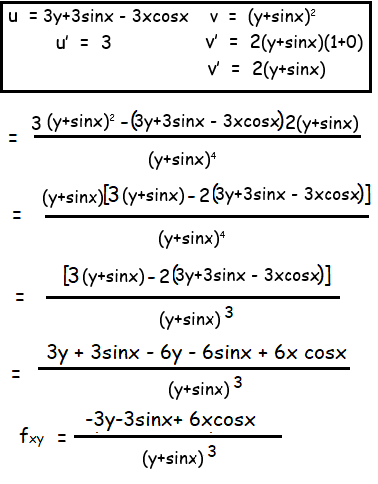
Finding f_y :

Differentiate with respect to y. Treat x as constant.

u = 3x and v = y+sinx

u' = 0 and v' = 1+0 ==> 1

f_y = [(y+sinx)(0) - 3x(1)]/(y+sinx)²

f_y = -3x/(y+sinx)²

Finding f_yx :

Differentiate with respect to x. Treat y as constant.

u = -3x, v = (y+sinx)²

u' = -3 and v' = 2((y+sinx))cosx

v' = 2cosx(y+sinx)

= [-3(y+sinx)² -(-3x) 2((y+sinx))cosx]/(y+sinx)⁴

= (y+sinx)[-3(y+sinx)+6xcosx]/(y+sinx)⁴

f_yx = [-3y-3sinx+6xcosx]/(y+sinx)³

Problem 2 :

f(x, y)  =  tan^-1(x/y)

Solution :

f(x, y)  =  tan^-1(x/y)

Finding f_x :

Differentiate with respect to x. Treat y as constant.

f_x = 1/(1+(x/y)²) (1/y)

f_x = (1/y)/(y²+x²)/y²

f_x = y/(x²+y²)

Finding f_xy :

Differentiate with respect to y. Treat x as constant.

u = y and v = x²+y²

u' = 1 and v' = 2y

f_xy  =  [x²+y²-y(2y)]/(x²+y²)

f_xy  =  (x²-y²)/(x²+y²)  ---(1)

f(x, y)  =  tan^-1(x/y)

Finding f_y :

f(x, y)  =  tan^-1(xy^-1)

Differentiate with respect to y. Treat x as constant.

f_y = [1/1+(x/y)²](-x/y²)

f_y = [y²/(x²+y²)](-x/y²)

f_y = -x/(x²+y²)

Finding f_yx :

Differentiate with respect to x. Treat y as constant.

u = -x and v = x²+y²

u' = -1 and v' = 2x

f_yx = [(x²+y²)(-1) - (-x)(2x)]/(x²+y²)²

f_yx = [-x²-y² +2x²]/(x²+y²)²

f_yx = (x²-y²)/(x²+y²)² ---(2)

Problem 3 :

f(x, y) = cos (x²-3xy)

Solution :

Finding f_x :

Differentiate with respect to x. Treat y as constant.

f_x = sin (x²-3xy)(2x-3y)

f_x = (2x-3y)sin (x²-3xy)

Finding f_xy :

u = 2x-3y and v = sin (x²-3xy)

u' = 0-3 and v' = cos (x²-3xy) (0-3x)

v' = -3xcos (x²-3xy)

f_{xy =} (2x-3y)(-3xcos) (x²-3xy) + sin (x²-3xy)(-3)

f_{xy =} (2x-3y)(-3xcos) (x²-3xy) + sin (x²-3xy)(-3)

f_xy = (2x-3y)(-3xcos) (x²-3xy) - 3 sin (x²-3xy)  --(1)

Finding f_y :

Differentiate with respect to y. Treat x as constant.

f_y = sin (x²-3xy)(0-3x)

f_y = -3x sin (x²-3xy)

Finding f_yx :

Differentiate with respect to x. Treat y as constant.

u = -3x and v = sin (x²-3xy)

u' = -3 and v' = cos (x²-3xy) (2x-3y)

f_yx = -3x cos (x²-3xy) (2x-3y) -3 sin (x²-3xy) --(2) 

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.