FIND DERIVATIVES OF RADICAL FUNCTIONS

To find the derivative of a radical function, first write the radical sign as exponent and find derivative using chain rule. 

Example :

f(x) = √x

f(x) = x^1/2

Find derivative with respect to x.

f'(x) = (1/2)x^1/2-1(x')

f'(x) = (1/2)x^-1/2(1)

= (1/2)(1/x^1/2)

= (1/2)(1/√x)

= 1/(2√x)

Base on the above example, we can derive formula for derivative of a radical function.

Let f(x) = √z. Then derivative f(x) : 

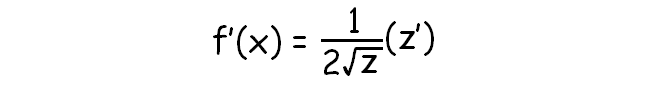
Find the derivative of the following radical functions with respect to x :

Example 1 :

y = √(x + 2)

Solution :

y = √(x + 2)

y' = {1/[2√(x + 2)]}(x + 2)'

y' = {1/[2√(x + 2)]}(1)

y' = 1/[2√(x + 2)]

Example 2 :

y = √(2x - 1)

Solution :

y = √(2x - 2)

y' = {1/[2√(2x - 1)]}(2x - 1)'

y' = {1/[2√(2x - 1)]}(2)

y' = 1/√(2x - 1)

Example 3 :

y = √(3x² + 5)

Solution :

y = √(3x² + 5)

y' = {1/[2√(3x² + 5)]}(3x² + 5)'

y' = {1/[2√(3x² + 5)]}(6x)

= 3x/√(3x² + 5)

Example 4 :

y = √(2x⁴ + 2x - 1)

Solution :

y = √(2x⁴ + 2x - 1)

y' = {1/[2√(2x⁴ + 2x - 1)]}(2x⁴ + 2x - 1)'

y' = {1/[2√(2x⁴ + 2x - 1)]}(8x³ + 2)

= (4x³ + 1)/(√2x⁴ + 2x - 1)

Example 5 :

y = (x³ + 2x)√x

Solution :

y = (x³ + 2x)√x

Since two x terms are multiplied, we have to use the product rule to find the derivative.

Product rule :

(uv)' = uv' + u'v

y' = (x³ + 2x)(1/2√x) + (3x² + 2)√x

= (x³/2√x + 2x/2√x) + 3x²√x + 2√x

= (1/2)x^(3-1/2) + x^{(1 - 1/2)} + 3x^{(2 + 1/2)} + 2√x

= (1/2)x^5/2 + x^1/2 + 3x^5/2 + 2√x

= [(1/2) + 3]x^5/2 + √x + 2√x

  = (7/2)x^5/2 + 3√x

Example 6 :

y = (√x + 2x)/x² - 1

Solution :

y = (√x + 2x)/x² - 1

In the above function, we have variable x in both numerator and denominator.

So, we have to use the quotient rule to find the derivative 

Quotient rule :

(u/v)' = (vu' - uv')/v²

= [(x² - 1)(1/2√x + 2) - (√x + 2x) (2x)]/(x² - 1)²

Example 7 :

y = x^3  5√(2 - x)

Solution :

y = x^3  5√(2 - x)

Let u = x³  and v = (2 - x)^1/5

u' = 3x² and v' = 1/5 (2 - x)^{1/5 - 1}

v' = 1/5 (2 - x)^-4/5

d(uv) = uv' + vu'

= x³ (1/5) (2 - x)^-4/5 + (2 - x)^1/5 (x³)

= x³ [1/5 (2 - x)^4/5] + (2 - x)^1/5

Example 8 :

y = √(2x - 5) / (7x - 9)

Solution :

y = √(2x - 5) / (7x - 9)

To remove square on both sides, 

y² = (2x - 5) / (7x - 9)

Using quotient rule, we find the derivative.

u = 2x - 5 and v = 7x - 9

u' = 2(1) - 0 and v' = 7(1) - 0

u' = 2 and v' = 7

2y(dy/dx) = [(7x - 9)(2) - (2x - 5)(7)] / (7x - 9)²

= [14x - 18 - (14x - 35)] / (7x - 9)²

= [14x - 18 - 14x + 35] / (7x - 9)²

2y(dy/dx) = 17/(7x - 9)²

(dy/dx) = (1/2y) [17/(7x - 9)²]

= (1/2√(2x - 5)/(7x - 9)) [17/(7x - 9)²]

= [√(7x - 9)/2√(2x - 5)] [17/(7x - 9)²]

Example 9 :

f(x) = ∛x² - 1/√x³

Solution :

f(x) = ∛x² - 1/√x³

f(x) = (x²)^1/3 - (x^-3)^1/2

f(x) = x^2/3 - x^-3/2

Differentiating with respect to x, we get

= (2/3) x^{(2/3) - 1} - (3/2) x^{(-3/2) - 1}

= (2/3) x^{(2 - 3)/3} - (3/2) x^{(-3 - 2)/2}

= (2/3) x^-1/3 - (3/2) x^-5/2

= [2/3 x^1/3] - [3/2x^5/2]

Example 10 :

f(x) = 2e^x √x

Solution ;

Given that, f(x) = 2e^x √x

Using product rulem, we find the derivative.

u = e^x  and v = √x

u' = e^x  and v' = 1/2√x

d(uv) = uv' + vu'

= e^x (1/2√x) + √xe^x 

Factroing e^x, we get

= e^x [1/2√x + √x]

= e^x (1 + 2x)/2√x

Example 11 :

Find f'(x) if f(x) = 1/∛(x² + x + 1)

Solution ;

f(x) = 1/∛(x² + x + 1)

f(x) = (x² + x + 1)^-1/3

f '(x) = -(1/3)(x² + x + 1)^{(-1/3) - 1} (2x + 1)

f '(x) = -(1/3)(2x + 1) (x² + x + 1)^(-4/3)

= -[1/3(2x + 1) (x² + x + 1)^4/3]

Example 12 :

Find f'(x) if f(x) = x/√(7 - 3x)

Solution ;

f(x) = x/√(7 - 3x)

u = x and v = √(7 - 3x) 

u' = 1 and v' = 1/2√(7 - 3x) (0 - 3 (1))

v' = -3/2√(7 - 3x)

d(u/v) = (vu' - uv') / v²

= (√(7 - 3x) (1) - x (-3/2√(7 - 3x))) / [√(7 - 3x)]²

= (2(7 - 3x)  + 3x) /2√(7 - 3x)) / (7 - 3x)

= (14 - 6x + 3x)/2(7 - 3x)√(7 - 3x)

f'(x) = (14 - 3x)/2(7 - 3x)√(7 - 3x)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.