FIND BINOMIAL EXPANSION OF RATIONAL FUNCTIONS

Find Binomial Expansion Of Rational Functions :

Here we are going to see some practice questions on finding binomial expansion of rational functions.

Formula for expansion of rational functions

(1 + x)ⁿ

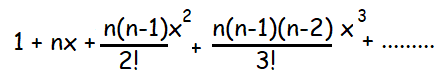
(1 - x)ⁿ

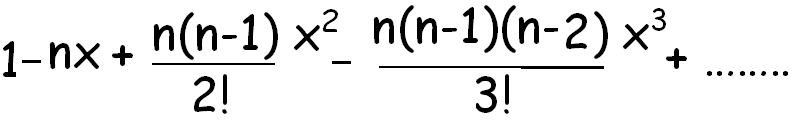
(1 + x)^-n

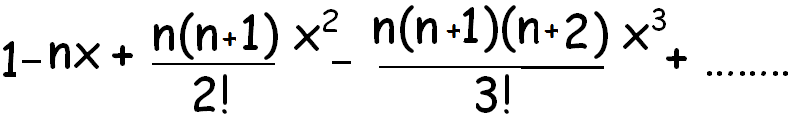
(1 - x)^-n

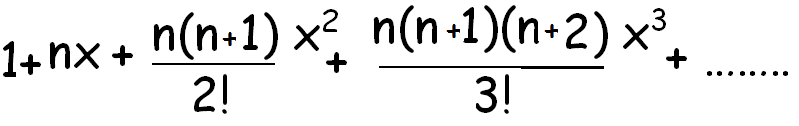
Note :

• When we have negative signs for either power or in the middle, we have negative signs for alternative terms.
• If we have negative for power, then the formula will change from (n - 1) to (n + 1) and (n - 2) to (n + 2).
• If we have negative signs for both middle term and power, we will have a positive sign for every term.

Observation of the coefficient in each of such expansions will be very helpful in solving problems. Let us list some of them:

1. (1 + x)⁻¹ = 1− x + x² − x³ + · · ·

2. (1 − x)⁻¹ = 1+x + x² + x³ + · · ·

3. (1 − x)⁻² = 1 + 2x + 3x² + 4x³ + 5x⁴ + 6x⁵ + · · ·

4. (1 + x)⁻² = 1− 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + · · ·

All the above expansions are valid only when |x| < 1.

Question 1 :

Expand the following in ascending powers of x and find the condition on x for which the binomial expansion is valid. 

(i)  1/(5 + x)

Solution :

1/(5 + x)  =  (1/5)(1 + (x/5))^-1 

x  =  x/5     |x| < 5

(1 + x)⁻¹ = 1− x + x² − x³ + · · ·

  =  (1/5) [1 - (x/5) + (x/5)² - (x/5)³ + .............]

  =  (1/5) [1 - (x/5) + (x²/25) - (x³/125) + .............]

(ii)  2/(3 + 4x)²

Solution :

 2/(3 + 4x)²  =  2 (3 + 4x)^-2

  =  2 (3 + 4x)^-2

(1 + x)⁻² = 1− 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + · · ·

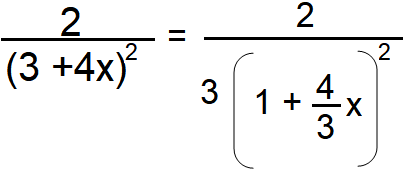
 =  (2/3)[ (1− 2(4/3) + 3(4x/3)² − 4(4x/3)³  + ............]

(iii)  (5 + x²)^2/3

Solution :

  =  5^2/3 (1 + x²/5)^2/3

1^st term  =   1

2^nd term  = nx  =  (2/3)(x²/5)  =  2x²/15

3^rd term  = (n(n-1)/2!)x²  =  [(2/3)(-1/3)/2!](x²/5)² 

  =  -x⁴/225

4^th term  = (n(n-1)(n-2)/3!)x³ 

=  [(2/3)(-1/3)(-4/3)/3!](x²/5)³ 

  =  4x⁶/(81 ⋅ 125)

=  1 + (2x²/15) - (x⁴/225) + 4x⁶/(81 ⋅ 125) + ................

Required condition is |x²| < 5

(iv)  (x + 2)^-2/3

Solution :

  =  (2 + x)^-2/3  =  2^-2/3 (1 + x/2)^-2/3

1^st term  =   1

2^nd term  = nx  =  (-2/3)(x/2)  =  -x/3

3^rd term  = (n(n-1)/2!)x²  =  [(-2/3)(-5/3)/2!](x/2)² 

  =  5x²/36

4^th term  = (n(n-1)(n-2)/3!)x³ 

=  [(-2/3)(-5/3)(-8/3)/3!](x/2)³ 

  =  -5x³/81

=  1 - (x/3) + (5x²/36) - (5x³/81) + ................

Required condition is |x| < 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.