FIND BALANCE ON INVESTMENT AFTER N YEARS INVOLVING COMPOUND INTEREST
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
We can define the compound interest as the interest accrues when earning for each specified period of time added to the principal thus increasing the principal base on which subsequent interest is computed.
A = P(1 + r/n)nt
A ----> Accumulated value (final value)
P ----> Principal (initial value of an investment)
r ----> Annual interest rate (in decimal)
n ----> Number of times interest compounded per year
t ----> Time (in years)
Example 1 :
An investor deposits $70 on the first day of each month into an account that pays 2% interest per annum compounded monthly. What is the balance of this annuity at the end of 4 years?
Solution :
We need to consider each of the 48 deposits separately.
The first deposit gains interest for 48 months, the second month deposit gains interest for 47 months and so on.
So the last month deposit (48 month's deposit) will give us only 1 month interest.
Principal = $70, Rate of interest (r) = 2% = 0.02
Interest is compounding monthly
1 year = 12 months
4 years = 48 months
A = P(1 + r/n)nt
The first deposit is gaining interest for 48 months.
A = 70 [1 + (0.02/12)]48
A = 70 [1 + (0.02/12)]48
The second deposit is gaining interest for 47 months.
A = 70 [1 + (0.02/12)]47
A = 70 [1 + (0.02/12)]47
.....
......
The last deposit is gaining interest for 1 month.
A = 70 [1 + (0.02/12)]1
A = 70 [1 + (0.02/12)]1
By writing these amounts as sequence we get
70 [1 + (0.02/12)]1, 70 [1 + (0.02/12)]2, 70 [1 + (0.02/12)]3,......... 70 [1 + (0.02/12)]48
This is a geometric sequence having the common ratio [1 + (0.02/12)]
a = 70 [1 + (0.02/12)] and r = [1 + (0.02/12)]
sn = a(1 - rn)/(1 - r)
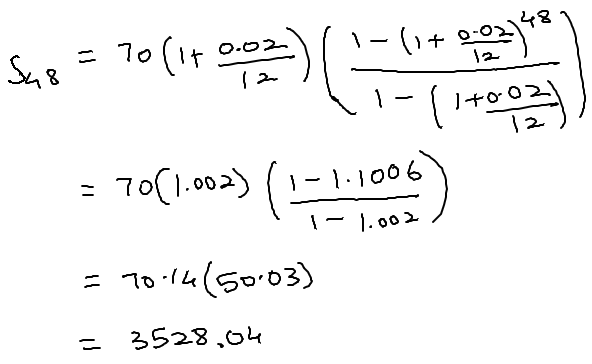
Example 2 :
Mrs. Bright has decided to retire as soon as she has set aside $1 million if she invests $10,000 in an account that earns 8.3% interest compound monthly
(a) How much money will she have in 20 years?
(b) How long will it be before she can retire?
Solution :
(a)
A = P(1 + r/n)nt
Principal = $10,000, r = 8.3%
n = 12(Compounding monthly), t = 20 years
A20 = 10000(1 + 0.083/12)12(20)
A20 = 52293.42
(b) To find the time consumption to reach the cost $1 million
1000000 = 10000(1 + 0.083/12)12t
100 = (1.0069)12t
log 100 = 12t log(1.0069)
2 = 12t(0.0029)
689.65 = 12t
t = 57 years
Example 3 :
An investor deposits $100 on the first day of each month in an account pays 1.8% interest compounded monthly. Find the balance in the account after 5 years.
Solution :
The investor is going to deposit $100 on each month.
1 year = 12 months
5 years = 60 months
The first month deposit is going to earn 60 months interest. If we calculate the value of 100 that is invested today after 60 months, we should use the formula given below.
A = P(1 + r/n)nt
The amount after 60 months after depositing $100 for the first month.
A = 100(1 + 0.018/12)60
The amount after 59 months after depositing $100 for the second month.
A = 100(1 + 0.018/12)59
..............
A = 100(1 + 0.018/12)1
Total balance = 100(1 + 0.018/12)1 + 100(1 + 0.018/12)2 +
................. + 100(1 + 0.018/12)60
a = 100(1 + 0.018/12), r = (1 + 0.018/12) and n = 60
sn = a(1 - rn)/(1 - r)
sn = 100(1 + 0.018/12)[1 - (1 + 0.018/12)60)/(1 - (1+0.018/12)]
= $6282.78
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions -
10 Hard SAT Math Questions (Part - 36)
Nov 28, 25 09:55 AM
10 Hard SAT Math Questions (Part - 36)