FIND ARITHMETIC MEAN BY DIRECT METHOD WORKSHEET

Question 1 :

Calculate the Arithmetic mean of the following data by direct method.

Solution :

Arithmetic mean : 

= ∑fx/N

= 390/25

= 15.6

Question 2 :

The following data give the number of boys of a particular age in a class of 40 students. Calculate the mean age of the students

Solution :

Mean age of the students : 

= ∑fx/N 

= 618/40

= 15.45 years

Question 3 :

Calculate the Arithmetic mean of the following data:

Solution :

Arithmetic mean : 

= ∑fx/N

= 4635/103

= 45

Question 4 :

An examination was held to decide the award of scholarship. The weights of various subjects were different. The marks obtained by 3 candidates (out of 100) in each subject are given below:

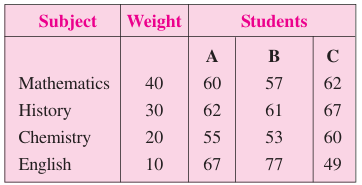
Calculate the weighted A.M. to award the scholarship.

Solution :

Σfx = 2400 + 1860 + 1100 + 670

= 6030

Σfx/Σf = 6030/100

= 60.3

Approximately 60

Σfx = 2280 + 1830 + 1060 + 770

= 5940

Σfx/Σf = 5940/100

= 59.4

Approximately 59

Σfx = 2480 + 2010 + 1200 + 490

= 6180

Σfx/Σf = 6180/100

= 61.8

Approximately 62.

So, student C should get scholarship.

Question 5 :

An environmentalist records the average temperatures of five regions.

a. Identify the outlier.

b. Which measure of central tendency will be most affected by removing the outlier?

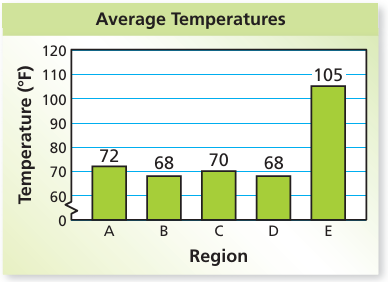
Solution :

a) The outlier is 105

b) 

Before removing outlier :

Mean = [72 + 70 + 2(68) + 105]/5

= 383/5

= 76.6

After removing outlier :

Mean = [72 + 70 + 2(68)]/4

= 278/4

= 69.5

Median :

Before removing outlier :

Arranging the data from least to greatest, we get

68, 68, 70, 72, 105

Median = 70

After removing outlier :

Arranging the data from least to greatest, we get

68, 68, 70, 72

Median = (68 + 70)/2

= 138/2

= 69

Mode is the maximum number of times the value is repeated. Then mode for the data is 68.

Mode is not affected. So, mean is affected much by removing the outlier.

Question 6 :

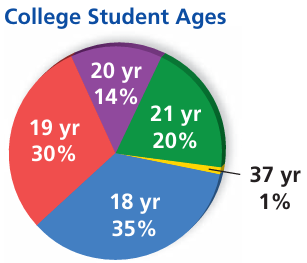
The circle graph shows the ages of 200 students in a college psychology class.

a. Find the mean, median, and mode of the students’ ages. Identify the outliers. 

b. How do the outliers affect the mean, median, and mode?

Solution :

Number of students whose age is 21 years :

= 20% of 200

= 0.20(200)

= 40

Number of students whose age is 20 years :

= 14% of 200

= 0.14(200)

= 28

Number of students whose age is 19 years :

= 19% of 200

= 0.19(200)

= 38

Number of students whose age is 18 years :

= 35% of 200

= 0.35(200)

= 70

Number of students whose age is 37 years :

= 1% of 200

= 0.01(200)

= 2

2, 28, 38, 40, 70

2 is the outlier.

a) Mean = (2 + 28 + 38 + 40 + 70)/5

= 178/5

= 35.6

Median = 38

Here is no mode.

b. After removing outlier :

By removing the outlier, finding mean

= (28 + 38 + 40 + 70)/4

= 44

Median = (38 + 40)/2

= 78/2

= 39

There is no mode.

Mean is affected.

Question 7 :

The mean of a certain number of observations is 40. If two or more items with values 50 and 64 are added to this data, the mean rises to 42. Find the number of items in the original data.

Solution :

Let n be the number of observations. 

Mean of n number of observations = 40

After adding 50 and 64, we get the new mean as 42

Σx/n = 40

(50 + 64 + 40n)/(n + 2) = 42

114 + 40n = 42(n + 2)

114 + 40n = 42n + 84

114 - 84 = 42n - 40n

30 = 2n

n = 30/2

n = 15

So, total number of elements is 15.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.