FIND ALL THE ZEROS AND WRITE A LINEAR FACTORIZATION

Find all of the zeros and write a linear factorization of the function

Problem 1 :

f(x) = x³ + 4x - 5

Solution :

Using synthetic division, let us find some of the factors of cubic polynomial.

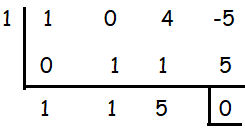
Using the above synthetic division, it is clear that 1 is solution.

The other two zeros can be figured out by solving the quadratic equation that we get here.

x² + x + 5 = 0

This quadratic equation cannot be solved using the method of factorization.

a = 1, b = 1 and c = 5

b² - 4ac = 1² - 4(1)(5)

= 1 - 20

= -19 < 0

= - b ± √(b² - 4ac)/2a

= (-1 ± √-19)/2(1)

= (-1 ± i√19)/2

So, the zeros are 1, (-1 + i√19)/2, (-1 - i√19)/2

Linear factorization is 

(x - 1)(x + 1/2 - i√19/2), (x + 1/2 + i√19/2)

Problem 2 :

f(x) = x⁴ + x³ + 5x² - x - 6

Solution :

Using synthetic division, let us find some of the factors of cubic polynomial.

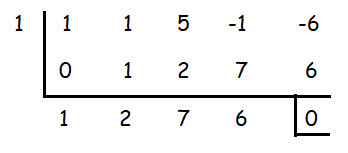
1 is a zero of the polynomial.

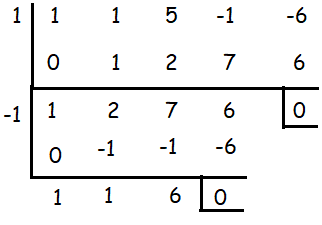
-1 is another zero, by solving the quadratic equation x² + x + 6 = 0, we get the other two zeroes.

x² + x + 6 = 0

This quadratic equation cannot be solved using the method of factorization.

a = 1, b = 1 and c = 6

b² - 4ac = 1² - 4(1)(6)

= 1 - 24

= -23 < 0

= - b ± √(b² - 4ac)/2a

= (-1 ± √-23)/2(1)

= (-1 ± i√23)/2

So, the zeros are 1, -1, (-1 + i√23)/2, (-1 - i√23)/2

Linear factorization is 

(x - 1)(x + 1) (x + 1/2 - i√23/2), (x + 1/2 + i√23/2)

Problem 3 :

f(x) = 3x⁴ + 8x³ + 6x² + 3x - 2

Solution :

Using synthetic division, let us find some of the factors of cubic polynomial.

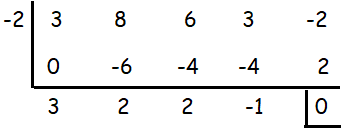
-2 is one zero of the polynomial, by solving the cubic polynomial

3x³ + 2x² + 2x - 1 = 0

we will get 3 zeroes.

Problem 4 :

Given that 4x⁴ + 17x² + 14x + 65 and the given one zero 1 - 2i find the remaining zeros of f(x)  and write in the factored form.

Solution :

Since the given zero is complex number, its conjugate be the other root.

Let α = 1 + 2i, then β = 1 - 2i

Using the above zeros, we can create a quadratic function which is having the highest exponent of 2.

The quadratic equation which consists of above zeros.

x² - (α + β)x + α  β = 0

x² - 2x + 5 = 0

The given polynomial f(x) will have 4 zeros. Two of the zeros is derived from the quadratic polynomial we have created. To find the other zeros, we divide the 4th degree polynomial by quadratic polynomial, so we get the quotient as other quadratic polynomial.

By solving the polynomial that we receive as quotient, we get the 

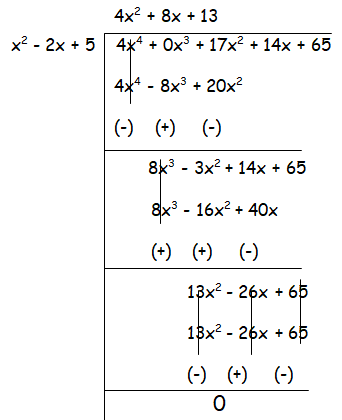
Quotient = 4x² + 8x + 13

This quadratic equation cannot be solved using the method of factorization.

a = 4, b = 8 and c = 13

b² - 4ac = 8² - 4(4)(13)

= 64 - 208

= -144 < 0

= - b ± √(b² - 4ac)/2a

= (-8 ± √-144)/2(4)

= (-8 ± i12)/8

= -1 ± i3/2

Solving the quotient, we get

-1 + i3/2, -1 - i3/2

So, the zeros are 1 + 2i, 1 - 2i, -1 + 3i/2 and -1 - 3i/2

The linear factors are,

(x - (1 + 2i)) (x - (1 - 2i)) (x + 1 - 3i/2)(x + 1 + 3i/2)

Problem 5 :

Find the zeros of polynomial

x² + x + 1

Solution :

= x² + x + 1

This quadratic equation cannot be solved using the method of factorization.

a = 1, b = 1 and c = 1

b² - 4ac = 1² - 4(1)(1)

= 1 - 4

= -3 < 0

= - b ± √(b² - 4ac)/2a

= (-1 ± √-3)/2

= (-1 ± i√3)/2

The zeros are 

(-1 + i√3)/2,  (-1 - i√3)/2

Linear factorization is,

[x - (-1 + i√3)/2],  [x - (-1 - i√3)/2]

[x + (1/2) - (i√3/2)],  [x + (1/2) + (i√3/2)]

Problem 6 :

Find the zeros of polynomial

x³ - 27

Solution :

= x³ - 27

a³ - b³ = (a - b)(a² + ab + b²)

x³ - 3³ = (x - 3)(x² + x(3) + 3²)

= (x - 3)(x² + 3x + 9)

(x - 3)(x² + 3x + 9) = 0

x - 3 = 0 and x² + 3x + 9 = 0

x = 3 and 

This quadratic equation cannot be solved using the method of factorization.

a = 1, b = 3 and c = 9

b² - 4ac = 3² - 4(1)(9)

= 9 - 36

= -27 < 0

= - b ± √(b² - 4ac)/2a

= (-3 ± √-27)/2(1)

= (-3 ± i√27)/2

= (-3 ± 3i√3)/2

So, the zeros are 3, (-3 + 3i√3)/2 and (-3 - 3i√3)/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.