FACTORING CUBIC POLYNOMIALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Every cubic polynomial will have 3 factors. To find those factors, we follow the following steps.
Step 1 :
We can find one linear factor of the given cubic polynomial using synthetic division.
Step 2 :
At the end of the first step, we will have quadratic factors. By factoring the quadratic equation, we can get other two factors.
Step 3 :
List all three factors.
Factor the following cubic polynomials :
Example 1 :
x3 - 2x2 - 5 x + 6
Solution :
Step 1 :
Let p(x) = x3 - 2x2 - 5 x + 6
Step 2 :
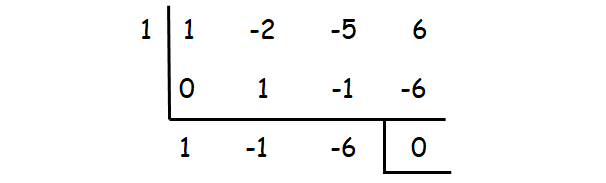
By dividing the cubic polynomial by 1, we get 0 as remainder. So (x - 1) is a factor.
We can get the other two factors, by factoring the quadratic polynomial x2 - x - 6.
x2 - x - 6 = (x - 3)(x + 2)
Step 3 :
The required factors are (x - 1) (x - 3) and (x + 2).
Example 2 :
4x3 - 7x + 3
Solution :
Step 1 :
Let p(x) = 4x3 - 7x + 3
Step 2 :
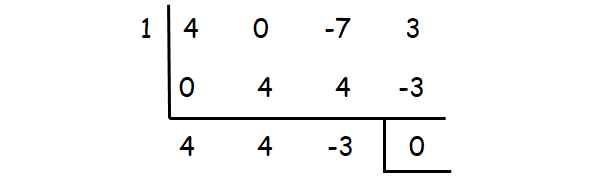
(x-1) is one of the factors.
We get the other two factors, by factoring the quadratic polynomial 4x2 + 4x -3.
= 4x2 + 6x - 2x - 3 (decomposing the middle term)
= 2x(2x + 3) - 1(2x + 3)
= (2x - 1)(2x + 3)
Step 3 :
So, the factors are (x - 1)(2x - 1)(2x + 3).
Example 3 :
x3 - 23x2 + 142x - 120
Solution :
Step 1 :
Let p(x) = x3 - 23x2 + 142x - 120
Step 2 :
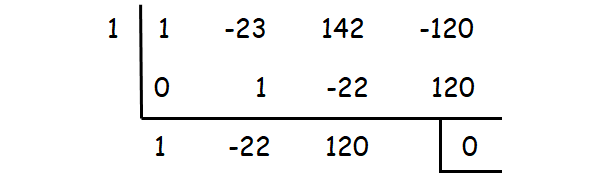
(x - 1) is a factor.
x2 - 22x + 120 = (x - 10)(x - 12)
Step 3 :
So, the factors are (x - 1)(x - 10)(x - 12).
Example 4 :
4x3 - 5x2 + 7x - 6
Solution :
Step 1 :
Let p(x) = 4x3 - 5x2 + 7x - 6
Step 2 :
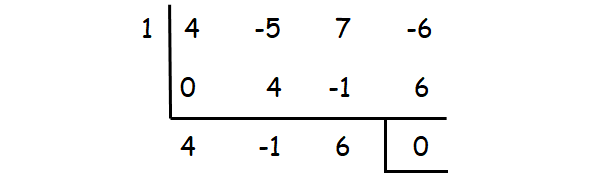
(x - 1) is one of the factors.
4x2 - x + 6 is not factorable.
Step 3 :
So, the factors are (x-1)(4x2-x+6).
Example 5 :
x3 - 7x + 6
Solution :
Step 1 :
Let p(x) = x3 - 7x + 6
Step 2 :
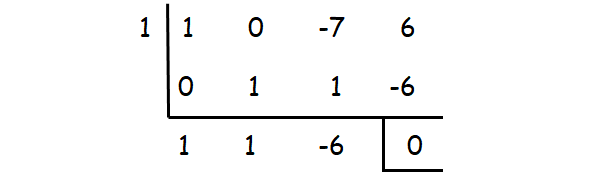
x2 + x - 6 = (x + 3)(x - 2)
Step 3 :
So, the factors are (x - 1)(x + 3)(x - 2).
Example 6 :
x3 + 13x2 + 32x + 20
Solution :
Step 1 :
Let p(x) = x3 + 13x2 + 32x + 20
Step 2 :
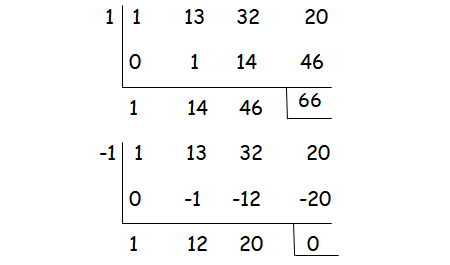
(x + 1) is one of the factors.
x2 + 12x + 20 = (x + 10)(x + 2)
Step 3 :
So, the factors are (x + 1)(x + 10)(x + 2).
Solving the following cubic equation.
Example 7 :
x3 + 7x2 + 11x + 5 = 0
Solution :
Step 1 :
Let p(x) = x3 + 7x2 + 11x + 5
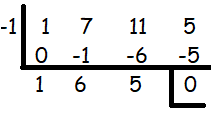
-1 is one of the solution.
Step 2 :
x2 + 6x + 5 = 0
x2 + 1x + 5x + 5 = 0
x (x + 1) + 5 (x + 1) = 0
(x + 5)(x + 1) = 0
Step 3 :
x + 5 = 0 and x + 1 = 0
x = -5 and x = -1
So, the three solutions are -1, -1 and -5.
Example 8 :
4x3 + 2x2 - 2x = 0
Solution :
Step 1 :
Let p(x) = 4x3 + 2x2 - 2x
4x3 + 2x2 - 2x = 0
Factoring 2x, we get
2x(2x2 + x - 1) = 0
2x(2x2 + 2x - 1x - 1) = 0
2x[2x (x + 1) - 1 (x + 1)] = 0
2x (2x - 1)(x + 1) = 0
Equating each factor to 0, we get
|
2x = 0 x = 0/2 x = 0 |
2x - 1 = 0 2x = 1 x = 1/2 |
x + 1 = 0 x = -1 |
So, the solutions are -1, 0 and 1/2
Example 9 :
-x3 - 3x2 + x + 3 = 0
Solution :
Step 1 :
Let p(x) = -x3 - 3x2 + x + 3
-x3 - 3x2 + x + 3 = 0
Factoring -x2, we get
-x2 (x + 3) + 1(x + 3) = 0
(x + 3)(-x2 + 1) = 0
Equating each factor to 0, we get
x + 3 = 0
x = -3
-x2 + 1 = 0
-x2 = -1
x2 = 1
x = -1 and 1
So, the solutions are -3, -1 and 1.
Example 10 :
The volume (in cubic feet) of a room in the shape of a rectangular prism is represented by 12z3 − 27z. Find expressions that could represent the dimensions of the room.
Solution :
Volume of rectangular prism = 12z3 − 27z
= 3z (4z2 - 9)
= 3z (22z2 - 32)
= 3z [(2z)2 - 32]
= 3z (2z + 3)(2z - 3)
Length = 3z, width = 2z + 3 and height = 2z - 3
Example 11 :
Factor the polynomial completely.
x3 + 2x2y − x − 2y
Solution :
= x3 + 2x2y − x − 2y
= x2 (x + 2y) - 1(x + 2y)
= (x2 - 1) (x + 2y)
= (x + 1)(x - 1) (x + 2y)
So, the factors are (x + 1)(x - 1) (x + 2y).
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37) -
Factorial Problems and Solutions
Dec 02, 25 09:27 AM
Factorial Problems and Solutions

