FACTORING POLYNOMIALS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Methods to Factor Polynomials
Any Polynomial—Look for the Greatest Common Factor :
xy - xz = x(y - z)
Example 1 :
6a2b + 10ab2 = 2ab(3a + 5b)
Binomials—Look for a Difference of Two Squares :
x2 - y2 = (x + y)(x - y)
Example 2 :
a2 - 9b2 = (a + 3b)(a - 3b)
Trinomials—Look for Perfect-Square Trinomials :
x2 + 2xy + y2 = (x + y)2
x2 - 2xy + y2 = (x - y)2
Examples 3 :
a2 + 4a + 4 = (a + 2)2
a2 - 2a + 1 = (a - 1)2
Other Factorable Trinomials :
x2 + bx + c = (x + _ ) (x + _ )
ax2 + bx + c = ( _ x + _ ) ( _ x + _ )
Examples 4 :
y2 + 3y + 2 = (y + 1)(y + 2)
6y2 + 7y + 2 = (2y + 1)(3y + 2)
Polynomials of Four or More Terms - Factor by grouping :
ax + bx + ay + by :
= x(a + b) + y(a + b)
= (x + y)(a + b)
Example 5 :
2y3 + 4y2 + y + 2 :
= (2y3 + 4y2) + (y + 2)
= 2y2(y + 2) + 1(y + 2)
= (y + 2)(2y2 + 1)
Note :
If none of the factoring methods work, the polynomial is unfactorable.
Remember :
For a polynomial of the form ax2 + bx + c, if there are no integers whose sum is b and whose product is ac, then the polynomial is unfactorable.
Factoring Polynomials
Recall that a polynomial is in its fully factored form when it is written as a product that cannot be factored further.
To factor a polynomial completely, you may need to use more than one factoring method. Use the steps below to factor a polynomial completely.
Step 1 :
Check for a greatest common factor.
Step 2 :
Check for a pattern that fits the difference of two squares or a perfect-square trinomial.
Step 3 :
To factor x2 + bx + c, look for two numbers whose sum is b and whose product is c.
To factor ax2 + bx + c, check factors of a and factors of c in the binomial factors. The sum of the products of the outer and inner terms should be b.
Step 4 :
Check for common factors.
Determining Whether an Expression is Completely Factored
Tell whether each expression is completely factored. If not, factor it.
Example 6 :
2a(a2 + 4)
Neither 2a nor a2 + 4 can be factored further.
2a(a2 + 4) is completely factored.
Example 7 :
(2a + 6)(a + 5)
2a + 6 can be further factored.
Factor out 2, the GCF of 2a and 6.
= 2(a + 3)(a + 5)
2(a + 3)(a + 5) is completely factored.
Factoring by GCF and Recognizing Patterns
Example 8 :
Factor -2ab2 + 16ab - 32a completely. Check your answer.
= -2ab2 + 16ab - 32a
Factor out the GCF.
= -2a(b2 - 8b + 16)
b2 + 8b + 16 is a perfect square trinomial of the form
x2 + 2xy + y2
x = b and y = 4.
= -2a(b - 4)2
Check :
-2a(b - 4)2 = -2a(b2 - 8b + 16)
= -2ab2 + 16ab - 32a ✓
Factoring by Multiple Methods
Factor each polynomial completely.
Example 9 :
2x2 + 5x + 4
The GCF is 1 and there is no pattern.
= ( _ x + _ ) ( _ x + _ )
a = 2 and c = 4; Outer + Inner = 5.
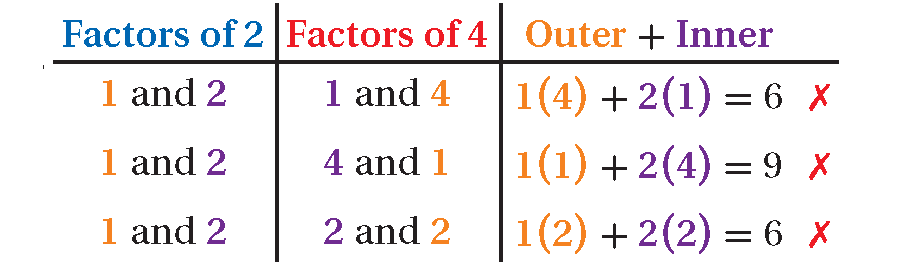
2x2 + 5x + 4 is unfactorable.
Example 10 :
3m4 - 15m3 + 12m2
Factor out the GCF.
= 3m2(m2 - 5m + 4)
There is no pattern.
= 3m2(m + _ )(m + _ )
b = -5 and c = 4; look for factors of 4 whose sum is -5.
|
Factors of 4 -1 and -4 |
Sum -5 ✓ |
The factors needed are -1 and -4.
= 3m2(m - 1)(m - 4)
Example 11 :
4y3 + 18y2 + 20y
Factor out the GCF.
= 2y(2y2 + 9y + 10)
There is no pattern.
= 2y( _ y + _ )( _ y + _ )
a = 2 and c = 10; Outer + Inner = 9
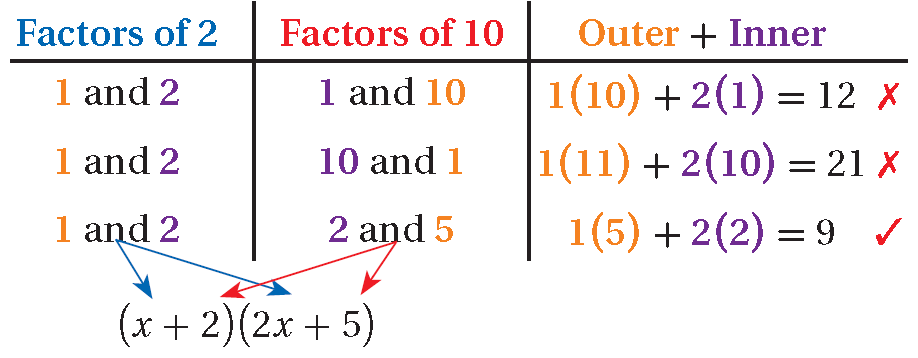
= 2y(y + 2)(2y + 5)
Example 12 :
n5 - n
Factor out the GCF.
= n(n4 - 1)
n4 - 1 is a difference of two squares.
= n(n2 + 1)(n2 - 1)
n2 - 1 is a difference of two squares.
= n(n2 + 1)(n + 1)(n - 1)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 38)
Dec 08, 25 12:12 AM
10 Hard SAT Math Questions (Part - 38) -
SAT Math Practice
Dec 05, 25 04:04 AM
SAT Math Practice - Different Topics - Concept - Formulas - Example problems with step by step explanation -
10 Hard SAT Math Questions (Part - 37)
Dec 03, 25 07:02 AM
10 Hard SAT Math Questions (Part - 37)


