FACTORING SPECIAL PRODUCTS

A trinomial is a perfect square if :

• The first and last terms are perfect squares.

• The middle term is two times one factor from the first term and one factor from the last term.

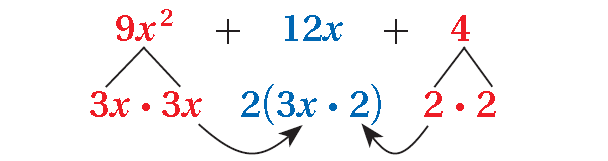
Perfect-Square Trinomials

a² + 2ab + b²  =  (a + b)(a + b)  =  (a + b)²

a² - 2ab + b²  =  (a - b)(a - b)  =  (a - b)²

Examples :

x² + 6x + 9  =  (x + 3)(x + 3)  =  (x + 3)²

x² -2x + 1  =  (x - 1)(x - 1)  =  (x - 1)²

Recognizing and Factoring Perfect-Square Trinomials

Determine whether each trinomial is a perfect square. If so, factor. If not, explain.

Example 1 :

x² + 12x + 36 

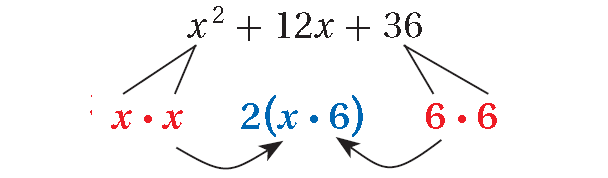
The trinomial is a perfect square. Factor.

Method 1 : Factor.

x² + 12x + 36

=  (x + 6)(x + 6)

=  (x + 6)²

Method 2 : Use the rule.

x² + 12x + 36

a = x, b = 6. 

Write the trinomial as a² + 2ab + b².

=  x² + 2(x)(6) + 6²

Write the trinomial as (a + b)².

=  (x + 6)²

Example 2 :

4x² - 12x + 9

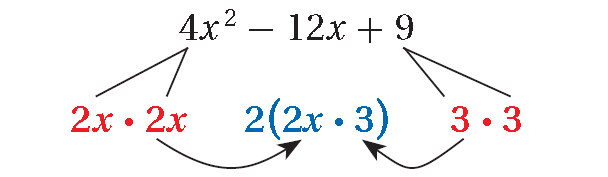
The trinomial is a perfect square. Factor.

=  4x² - 12x + 9

a = 2x, b = 3. 

Write the trinomial as a² - 2ab + b².

=  (2x)² - 2(2x)(3) + 3²

Write the trinomial as (a - b)².

=  (2x - 3)²

Example 3 :

x² + 9x + 16

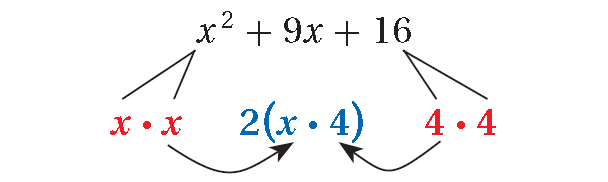
2(x · 4)  ≠  9x

x² + 9x + 16 is not a perfect-square trinomial because

9x  ≠  2(x · 4)

Difference of Two Squares

a² - b²  =  (a + b)(a - b)

Example : 

x² - 9  =  (x + 3)(x - 3)

The difference of two squares can be written as the product (a + b)(a - b) . You can use this pattern to factor some polynomials. 

A polynomial is a difference of two squares if:

• There are two terms, one subtracted from the other.

• Both terms are perfect squares.

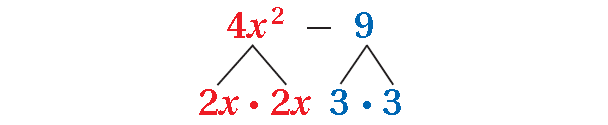
Recognizing and Factoring the Difference of Two Squares

Determine whether each binomial is a difference of two squares. If so, factor. If not, explain.

Example 4 :

x² - 81

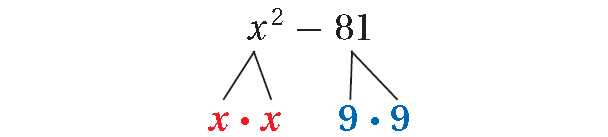
The polynomial is a difference of two squares.

=  x² - 81

=  x² - 9²

a = x and b = 9, write the polynomial as (a + b)(a - b).

=  (x + 9)(x - 9)

Example 5 :

9p⁴ - 16q²

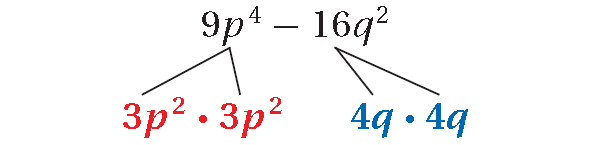
The polynomial is a difference of two squares.

=  9p⁴ - 16q²

=  (3p²)² - (4q)²

a = 3p² and b = 4q, write the polynomial as (a + b)(a - b).

=  (3p² + 4q)(3p² - 4q)

Example 6 :

x⁶ - 7y²

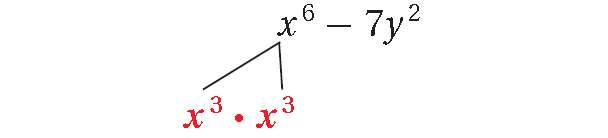
7y² is not a perfect square.

x⁶ - 7y² is not the difference of two squares because 7y² is not a perfect square.

Problem-Solving Application

Example 7 :

The park in the center of the Place des Vosges in Paris, France, is in the shape of a square. The area of the park is (25x² + 70x + 49) ft² . The side length of the park is in the form cx + d, where c and d are whole numbers. Find an expression in terms of x for the perimeter of the park. Find the perimeter when x = 8 ft.

Understand the Problem : 

The answer will be an expression for the perimeter of the park and the value of the expression when x = 8.

List the important information :

• The park is a square with area (25x² + 70x + 49) ft².

• The side length of the park is in the form cx + d, where c and d are whole numbers.

Make a Plan : 

The formula for the area of a square is area = (side) 2 .

Factor 25x² + 70x + 49 to find the side length of the park. Write a formula for the perimeter of the park, and evaluate the expression for x = 8.

Solve :

25x² + 70x + 49

a = 5x, b = 7. 

Write the trinomial as a² + 2ab + b².

=  (5x)² + 2(5x)(7) + 7²

Write the trinomial as (a + b)².

=  (5x + 7)²

25x² + 70x + 49  =  (5x + 7)(5x + 7)

The side length of the park is (5x + 7) ft.

Write a formula for the perimeter of the park.

P  =  4s

Substitute the side length for s.

=  4(5x + 7)

Distribute 4. 

=  20x + 28

An expression for the perimeter of the park in feet is 20x + 28.

Evaluate the expression when x = 8.

P = 20x + 28

Substitute 8 for x.

= 20 (8) + 28

= 188

When x = 8 ft, the perimeter of the park is 188 ft.

Look Back :

For a square with a perimeter of 188 ft, the side length is

188/4  =  47 ft

and the area is

47²  =  2209 ft²

Evaluate 25x² + 70x + 49 for x = 8. 

=  25(8)² + 70(8) + 49

=  16001 + 560 + 49

=  2209 ✓

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.