FACTORING QUADRATIC POLYNOMIALS
In this section, you will learn how to factor quadratic polynomial in the form ax2 + bx + c, where a ≠ 0.
When you multiply (3x + 2) (2x + 5), the coefficient of the x2-term is the product of the coefficients of the x-terms. Also, the constant term in the trinomial is the product of the constants in the binomials.
To factor a quadratic polynomial like ax2 + bx + c into its binomial factors, write two sets of parentheses :
( _ x + _ )( _ x + _ )
Write two numbers that are factors of a next to the x’s and two numbers that are factors of c in the other blanks. Then multiply to see if the product is the original quadratic polynomial. If there are not two such integers, the quadratic polynomial is unfactorable.
Factoring ax2 + bx + c by Guess and Check :
Example 1 :
Factor 4x2 + 16x + 15 by guess and check.
Solution :
Write two sets of parentheses.
( _ + _ )( _ + _ )
The first term is 4x2, so at least one variable term has a coefficient other than 1.
( _ x + _ )( _ x + _ )
The coefficient of the x2-term is 4. The constant term in the trinomial is 15.
Try factors of 4 for the coefficients and factors of 15 for the constant terms.
(1x + 15)(4x + 1) = 4x2 + 61x + 15 ✗
(1x + 5)(4x + 3) = 4x2 + 23x + 15 ✗
(1x + 3)(4x + 5) = 4x2 + 17x + 15 ✗
(1x + 1)(4x + 15) = 4x2 + 19x + 15 ✗
(2x + 15)(2x + 1) = 4x2 + 32x + 15 ✗
(2x + 5)(2x + 3) = 4x2 + 16x + 15 ✓
The factors of 4x2 + 16x + 15 are (2x + 5) and (2x + 3).
So, to factor ax2 + bx + c, check the factors of a and the factors of c in the binomials. The sum of the products of the outer and inner terms should be b.
Since you need to check all the factors of a and all the factors of c, it may be helpful to make a table. Then check the products of the outer and inner terms to see if the sum is b. You can multiply the binomials to check your answer.
Factoring ax2 + bx + c When c is Positive :
Factor each quadratic polynomial. Check your answer.
Example 2 :
2x2 + 11x + 12
Solution :
a = 2 and c = 12; Outer + Inner = 11.
( _ x + _ )( _ x + _ )
Check :
Use the FOIL method.
(x + 4)(2x + 3) = 2x2 + 3x + 8x + 12
= 2x2 + 11x + 12 ✓
Example 3 :
5x2 - 14x + 8
Solution :
a = 5 and c = 8; Outer + Inner = -14.
( _ x + _ )( _ x + _ )
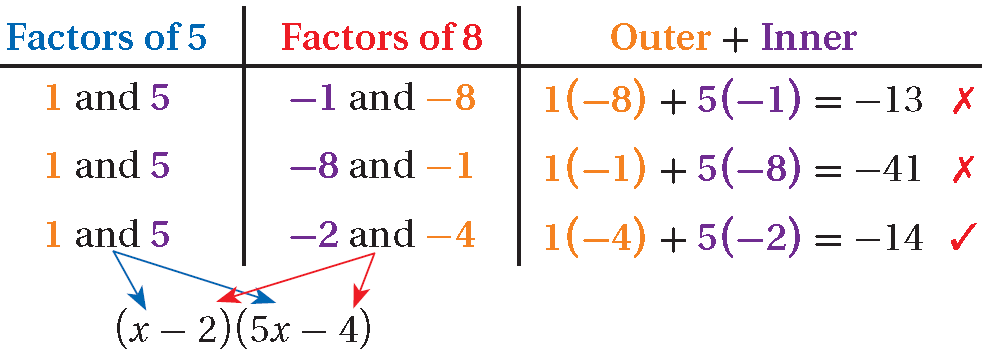
Check :
Use the FOIL method.
(x - 2)(5x - 4) = 5x2 - 4x - 10x + 8
= 5x2 - 14x + 8 ✓
When c is negative, one factor of c will be positive and the other factor will be negative. Only some of the factors are shown in the examples, but you may need to check all of the possibilities.
Factoring ax2 + bx + c When c is Negative :
Factor each quadratic polynomial. Check your answer.
Example 4 :
4y2 + 7y - 2
Solution :
a = 4 and c = -2; Outer + Inner = 7.
( _ y + _ )( _ y + _ )
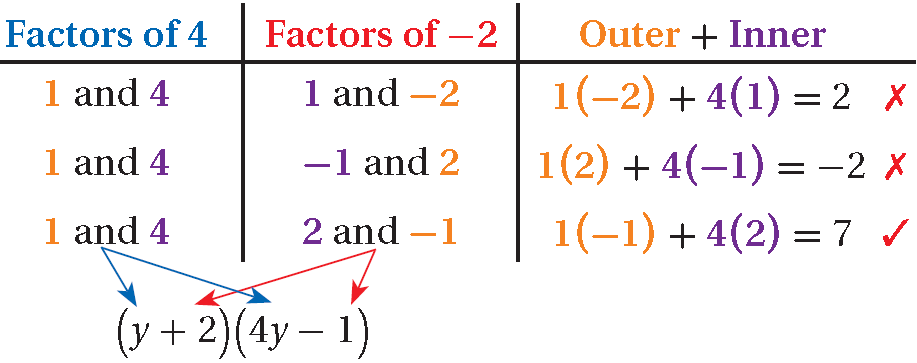
Check :
Use the FOIL method.
(y + 2)(4y - 1) = 4y2 - y + 8y - 2
= 4y2 + 7y - 2 ✓
Example 5 :
4x2 + 19x - 5
Solution :
a = 4 and c = -5; Outer + Inner = 19.
( _ x + _ )( _ x + _ )
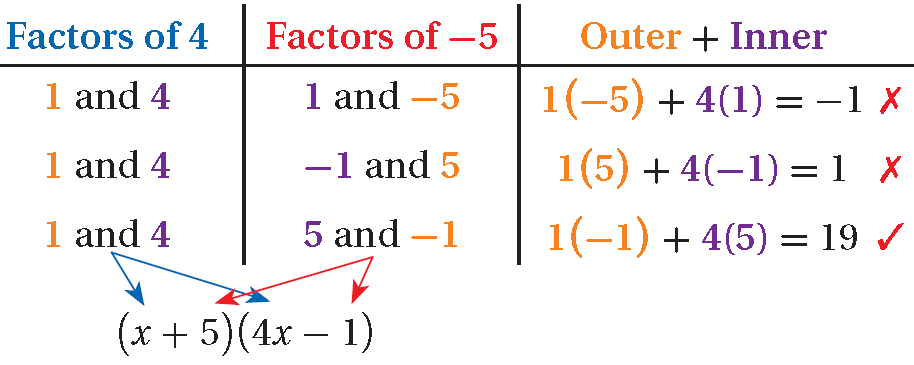
Check :
Use the FOIL method.
(x + 5)(4x - 1) = 4x2 - x + 20x - 5
= 4x2 + 19x - 5 ✓
Example 6 :
2x2 - 7x - 15
Solution :
a = 2 and c = -15; Outer + Inner = -7.
( _ x + _ )( _ x + _ )
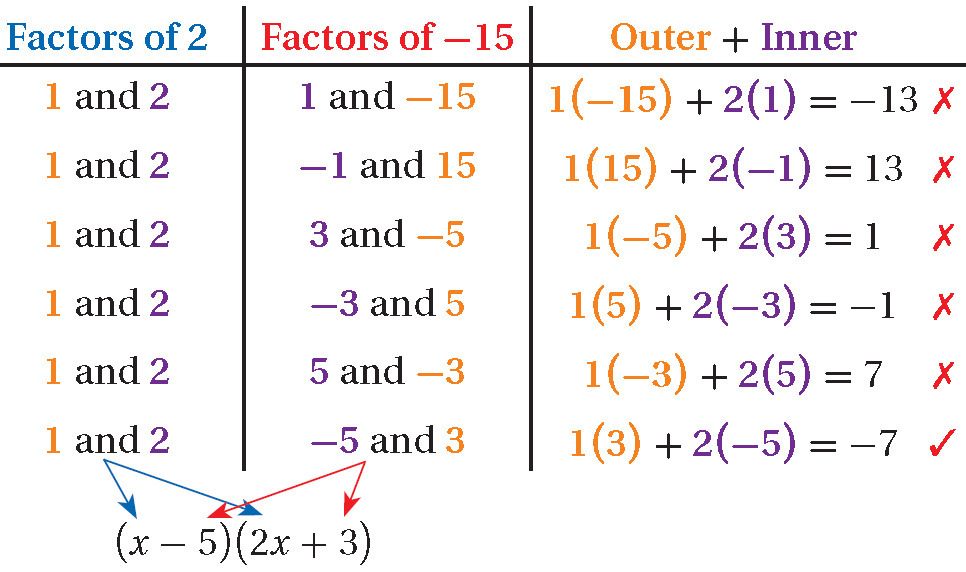
Check :
Use the FOIL method.
(x - 5)(2x + 3) = 2x2 + 3x - 10x + 15
= 2x2 - 7x + 15 ✓
When the leading coefficient is negative, factor out -1 from each term before using other factoring methods.
Example 7 :
Factor -2x2 - 15x - 7.
Solution :
Factor out -1.
= -1(2x2 + 15x + 7)
a = 2 and c = 7; Outer + Inner = 15.
( _ x + _ )( _ x + _ )
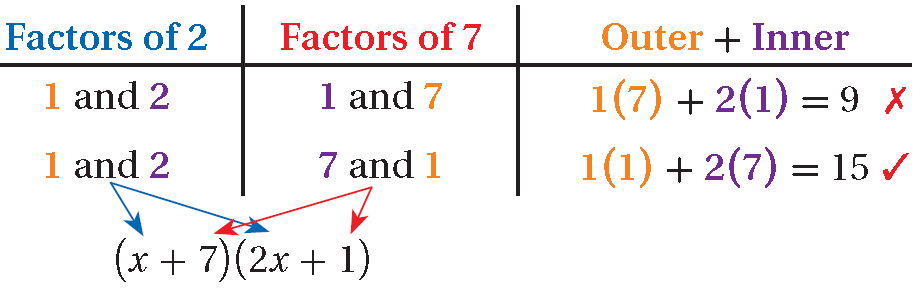
= -1(x + 7)(2x + 1)
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Recent Articles
-
AP Precalculus Problems and Solutions (Part - 1)
Oct 30, 24 10:07 AM
AP Precalculus Problems and Solutions (Part - 1) -
SAT Math Resources (Videos, Concepts, Worksheets and More)
Oct 29, 24 06:24 AM
SAT Math Resources (Videos, Concepts, Worksheets and More) -
Digital SAT Math Problems and Solutions (Part - 61)
Oct 29, 24 06:23 AM
Digital SAT Math Problems and Solutions (Part - 61)