EXPRESS THE GIVEN RATIO IN SIMPLEST FORM

Example 1 :

Express the following ratio in the simplest form :

(i)  8 : 16

(ii)  35 : 20

(iii)  2/5 : 3/5

(iv)  1   1/2 : 5

(v)  3 : 1  1/2

(vi)  2  1/2 : 1  1/2

(vii)  0.05 : 0.15

(viii)  0.18 : 0.06

Solution :

(i)  8 : 16

When we divide by 8, we get

=  8/8 : 16/8

=  1 : 2

So, the simplest form is 1 : 2.

(ii)  35 : 20

=  35/5 : 20/5

=  7 : 4

So, the simplest form is 7 : 4.

(iii)  2/5 : 3/5

By multiplying both parts by 5, we get

=  (2/5)⋅5 : (3/5) ⋅ 5

=  2 : 3

So, the simplest form is 2 : 3.

(iv)  1   1/2 : 5

Converting 1  1/2 as improper fraction, we get

3/2 : 5

Multiplying both parts by 2, we get

=  (3/2) ⋅ 2 : 5 ⋅ 2

=  3 : 5

So, the simplest form is 3 : 5.

(v)  3 : 1  1/2

Converting the second part 1  1/2 as improper fraction, we get

=  3 : 3/2

Multiplying both parts by 2, we get

=  3 ⋅ 2 : (3/2) ⋅ 2

=  6 : 3

Dividing by 3, we get 

=  2 : 1

So, the simplest form is 2 : 1.

(vi)  2  1/2 : 1  1/2

Changing the mixed numbers as improper fractions, we get

5/2 : 3/2

Multiplying by 2 on both sides, we get

=  5 : 3

So, the simplest form is 5 : 3.

(vii)  0.05 : 0.15

Multiplying both parts by 100, we get

=  5 : 15

Dividing by 5 on both sides, we get

=  1 : 3

So, the simplest form is 1: 3.

(viii)  0.18 : 0.06

Multiplying both parts by 100, we get

=  18 : 6

Dividing both parts by 6, we get

=  3 : 1

So, the simplest form is 3 : 1.

Example 2 :

Express as a ratio in simplest form :

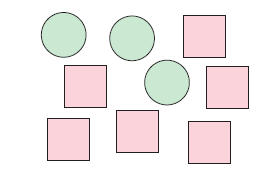
a) the number of circles to squares

(b)  cats to mice

(c)  Teachers to students 

(d)  Trees and flowers

Solution :

(a)  Number of circles  =  3

Number of squares  =  6

Number of circles : Number of squares  =  3 : 6

=  1 : 2

So, circles and squares are in the ratio 1 : 2.

(b)  Number of cats  =  2 and number of mice  =  3

Number of cats : number of mice  =  2 : 3

(c)  Number of teacher  =  1, number of students  =  7

Number of teachers : Number of students  =  1 : 7

(d)  Number of trees  =  3, number of flowers  =  8

Number of teachers : Number of students  =  3 : 8

Example 3 :

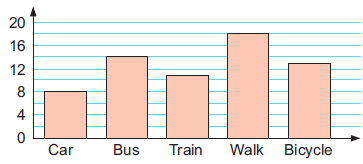
The column graph represents the results of a survey to determine the method by which students travel to school.

a) Find the total number of students surveyed.

b) Write as a ratio :

i) students arriving by car : students who walk

ii) students arriving by bus : total number of students surveyed.

c) What fraction of the students surveyed travel to school by bus?

Solution :

a) By observing the bar graphs, we know that number of students travel to school

by car = 8

by bus = 14

by train = 11

by walk = 16

by bicycle = 14

Total number of students = 8 + 14 + 11 + 16 + 14

= 63

Find the total number of students surveyed = 63

b) 

i) students arriving by car : students who walk

= 8 : 16

= 1 : 2

ii) students arriving by bus : total number of students surveyed.

= 14 : 63

= 2 : 9

c) Total number of students = 63

number of students travel by bus = 14

Representing as fraction = 14/63

= 2/9

Example 4 :

Express as a ratio in simplest form:

a) 20 cents to $1

b) $3 to 60 pence

c) 15 kg to 30 kg

d) 13 cm to 26 cm

Solution :

a) 20 cents to $1

$1 = 100 cents

The quantities are not in the same kind.

= 20 : 100

= 20/100

= 1/5

= 1 : 5

b) £3 to 60 pence

Since the given quantities are not in same kind, doing some conversion we can make it in the same kind.

100 pence = £1

= 300 : 60

= 300/60

= 5/1

= 5 : 1

c) 15 kg to 30 kg

Since the quantities are in same kind, we dont have to do any conversion.

= 15 : 30

= 15/30

= 1/2

d) 13 cm to 26 cm

= 13 : 26

= 13/26

= 1/2

= 1 : 2

So, the required ratio is 1 : 2.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.