EXPRESS THE FOLLOWING IN SIMPLEST EXPONENTIAL FORM

What is exponential form ?

The exponential form is a shortcut way of writing repeated multiplication involving base and exponents.

For example :

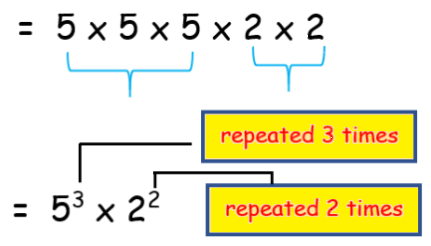
In this form, the power represents the number of times we are multiplying the base by itself.

Sometimes it may necessary to use the rules of exponents. 

Express in simplest form with a prime number base :

Problem 1 :

4

Solution :

Decompose 4 into prime factors.

4 = 2×2

2 is repeated 2 times.

= 2² 

Problem 2 :

16

Solution :

Decompose 16 into prime factors.

16 = 2×2×2×2

2 is repeated 4 times.

= 2⁴ 

Problem 3 :

27

Solution :

Decompose 27 into prime factors.

27 = 3×3×3

3 is repeated 3 times.

= 3³ 

Problem 4 :

4²

Solution :

4² = (2×2)²

2 is repeated 2 times.

= (2²)²

By using power rule (a^m)ⁿ = a^mn, we get

= 2⁴  

Problem 5 :

25²

Solution :

25² = (5×5)²

5 is repeated 2 times.

= (5²)²

By using power rule (a^m)ⁿ = a^mn, we get

= 5⁴ 

Problem 6 :

2^t × 8

Solution :

Decompose 8 into prime factors.

8 = 2×2×2

= 2^t × 8

= 2^t×2×2×2

2 is repeated 3 times.

= 2^t × 2³

By using product rule a^m × aⁿ = a^m+n, we get

= 2^{t + 3}

Problem 7 :

3^a ÷ 3

Solution :

= 3^a ÷ 3

= 3^a ÷ 3¹

By using quotient rule a^m ÷ aⁿ = a^m-n, we get

= 3^{a – 1} 

Problem 8 :

2ⁿ × 4ⁿ

Solution :

= 2ⁿ × 4ⁿ

= 2ⁿ×(2×2)ⁿ

= 2ⁿ × (2²)ⁿ

= (2)ⁿ × (2)²ⁿ

By using product rule a^m × aⁿ = a^m+n, we get

= 2^{n+ 2n}

= 2³ⁿ 

Problem 9 :

9/(3^x)

Solution :

= 9/(3^x)

= (3²)/(3^x)

By using quotient rule a^m/aⁿ = a^m-n, we get

= 3^{2 – x}

Problem 10 :

5ⁿ⁺²/5^n–2

Solution :

= 5ⁿ⁺²/5^n–2

By using quotient rule a^m/aⁿ = a^m-n, we get

= 5^{(n+2)–(n–2)}

= 5^n+2-n+2

= 5²⁺²

= 5⁴

Problem 11 :

(3⁴)^a+1

Solution :

= (3⁴)^a+1

By using power rule (a^m)ⁿ = a^mn, we get

= 3^{(4a + 4)} 

Problem 12 :

3^x × 3^4-x

Solution :

= 3^x × 3^4–x

By using product rule a^m × aⁿ = a^m+n, we get

= (3)^x+4–x

= 3⁴ 

Problem 13 :

(4^a)/2^b

Solution :

= (4^a)/2^b

= (2 × 2)^a/2^b

= (2²)^a/2^b

= 2^2a/2^b

By using quotient rule a^m/aⁿ = a^m-n, we get

= 2^{(2a – b)} 

Problem 14 :

8^x/16^y

Solution :

8^x/16^y = (2 × 2 × 2)^x/(2 × 2 × 2 × 2)^y

= (2³)^x/(2⁴)^y

 = 2^3x/2^4y

By using quotient rule a^m/aⁿ = a^m-n, we get

= 2^{3x – 4y} 

Problem 15 :

5^1+x /5^x-1

Solution :

= 5^1+x/5^x–1 

By using quotient rule a^m/aⁿ = a^m-n, we get

= 5^1+x-x+1

= 5²

Problem 16 :

(3^a × 9^a)/27^a+2

Solution :

= (3^a × (3²)^a)/(3³) ^{a + 2}

= (3^a × 3^2a)/3^3a+6

= 3^a+2a/3^3a+6

= 3^a+2a-3a-6

= 3^a-a-6

= 3^-6

= 1/3⁶

Problem 17 :

The following numbers can be written in the form 2ⁿ. Find n.

a)  32      b)  256     c)  4056

Solution :

a)  32

Decomposing 32 using prime numbers,

32 = 2 x 2 x 2 x 2 x 2

= 2⁵

b)  256

Decomposing 256 using prime numbers,

256 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2

= 2⁸

c)  4056

Decomposing 4096 using prime numbers,

4096 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2

= 2¹²

Problem 18 :

By considering 3¹, 3², 3³, 3⁴, ............... and looking for a pattern, find the last digit of 3³³

Solution :

3¹ = 3

3² = 9

3³ = 27

3⁴ = 81

3⁵ = 243

3⁶ = 729

By observing the pattern above, we know that the cyclicity of 3 is 4. Since we have power 33, dividing 33 by the cyclcity of 3 which is 4, we get 1 as remainder. Then 3 should be the unit digit 3³³

Problem 19 :

What is the last digit of 7⁷⁷

Solution :

7⁷⁷

Let us find the cyclicity of 7,

7¹ = 7

7² = 49

7³ = 343

7⁴ = 2401

By observing the pattern above, we know that the cyclicity of 7 is 4. Since we have power 77, dividing 77 by the cyclcity of 7 which is 4, we get 1 as remainder. Then 7 should be the unit digit 7⁷⁷

Problem 20 :

Find n, if 

a) 5⁴  = n      b)  n³ = 343      c)  11ⁿ = 161051

Solution :

a) 5⁴  = n

Since we have power 4 for 5, we have to multiply 5 four times. Then 

5 x 5 x 5 x 5  = n

n = 625

b)  n³ = 343

In the left side we have n³, so we will try to express 343 also in exponential form. 

343 = 7 x 7 x 7

n³ = 7³

c)  11ⁿ = 161051

In the left side we have n³, so we will try to express 161051 also in exponential form. 

161051 = 11 x 11 x 11 x 11 x 11

11ⁿ = 11⁵

By comparing the powers, the value n is 5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.