EXPONENTS WITH NEGATIVE BASES

In solving problems on exponents with negative base, we may have the following  two situations.

(i) Positive exponents with negative bases. 

(ii) Negative exponents with negative bases. 

Negative base will become positive if the power is even. Negative base will become negative if the power is odd.

Whenever we have a negative number as exponent and we need to make it as positive, we have to flip the base that is write the reciprocal of the base and change the negative exponent as positive exponent.

Positive Exponents with Negative Bases

When we do problems on positive exponents with negative bases, it is important to know the difference between

(-3)²   and   -3²

Order of operations (PEMDAS) dictates that parentheses take precedence.

So, we have

(-3)²  =  (-3) ⋅ (-3)

(-3)²  =  9

Without parentheses, exponents take precedence :

-3²  =  -3 ⋅ 3

-3²  =  -9

The negative is not applied until the exponent operation is carried through. We have to make sure that we understand this. So, we will not make this common mistake. 

Sometimes, the result turns out to be the same, as in. 

(-2)³   and   -2³

That is, 

(-2)³  =  (-2)(-2)(-2)  =  -8

(-2)³  =  - 2 ⋅ 2 ⋅ 2  =  -8

Result 1 :

If there is positive even exponent and negative sign inside the parenthesis, then the result is positive. 

Example : 

(-a)²  =  a²

Result 2 : 

If there is positive odd exponent and negative sign inside the parenthesis, then the result is negative. 

Example : 

(-a)²  =  a²

Negative Exponents with Negative Bases

Consider the following exponential form.

(-a)^-b

Here the base is '-a' and the exponent is '-b'.

To evaluate (-a)^-b, first we have to change the negative sign of the exponent as positive shown below. 

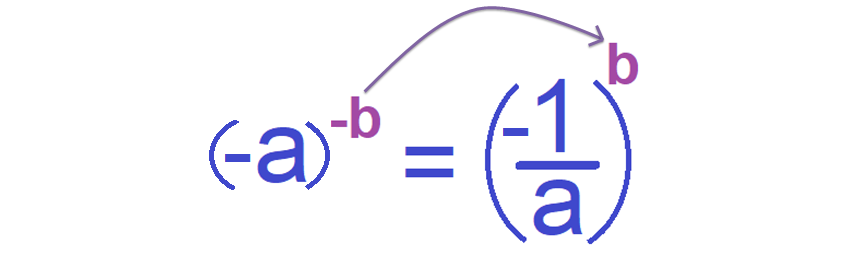
From the above example, it is clear that if there is a negative exponent for a base, the negative exponent can be changed as positive exponent by taking the reciprocal to the base.

We have to do further evaluation based on the exponent (even or odd). 

Solved Problems

Problem 1 :

Evaluate : 

-8²

Solution : 

=  -8²

=  - 8 ⋅ 8

=  - 64

Problem 2 :

Evaluate : 

(-8)²

Solution :

=  (-8)(-8)

=  64

Problem 3 :

Evaluate : 

(-8)³

Solution : 

= (-8)(-8)(-8)

= -512

Problem 4 :

Evaluate : 

-4³

Solution : 

=  - 4 ⋅ 4 ⋅ 4

=  -64

Problem 5 :

Evaluate : 

3^-2

Solution : 

=  3^-2

=  (1/3)²

Distribute the exponent to numerator and denominator. 

=  1² / 3²

=  1/9

Problem 6 :

Evaluate : 

(-3/2)^-2

Solution : 

=  (-3/2)^-2

=  (-2/3)²

Since the exponent is even, the negative sign inside the parentheses will become positive. 

=  (2/3)²

Distribute the exponent to numerator and denominator. 

=  2² / 3²

=  4/9

Problem 7 :

Evaluate : 

(-5/4)^-3

Solution : 

=  (-5/4)^-3

=  (-4/5)³

Since the exponent is odd, the negative sign inside the parentheses will remain same. 

Distribute the exponent to numerator and denominator. 

=  - 4³ / 5³

=  - 64/125

Problem 8 :

Evaluate :

(-5^-2) ⋅ (-3^-4)

Solution :

=  (-5^-2) ⋅ (-3^-4)

=  (-1/5)² ⋅ (-1/3)⁴

=  (1/25) ⋅ (1/81)

=  1/2025

Problem 9 :

Evaluate :

(-3)^-4/ (-2)^-3

Solution :

=  (-3)^-4/ (-2)^-3

=  (-1/3)⁴/ (-1/2)³

=  (1/81) / (-1/8)

=  (1/81) ⋅ (-8/1)

=  - 8/81

Problem 10 :

It is given that (-a)^-1/3  =  4/3. Find the value of a. 

Solution :

(-a)^-1/3  =  4/3

-a  =  (4/3)^-3/1

-a  =  (4/3)^-3

-a  =  (3/4)³

Distribute the exponent to numerator and denominator. 

-a  =  3³ / 4³

-a  =  27/64

Multiply each side by -1. 

a  =  - 27/64

Problem 11 :

Simplify [(-1/3)²]³ and express the result in exponential form.

Solution :

= [(-1/3)²]³

When we have power raised by another power, we have to multiply the powers.

= (-1/3)⁶

Since we have even number in the power, the negative can be changed as positive.

= (1/3)⁶

Problem 12 :

Simplify

(-4/5)^-2 x (-4/5)³ x[ (-4/5)^-1]²

Solution :

= (-4/5)^-2 x (-4/5)³ x[ (-4/5)^-1]²

Here the first two terms are having same base. Then we can put one base and combine the exponents.

= (-4/5)^-2+3 x [(-4/5)^-1]²

= (-4/5)¹ x (-4/5)^-2

Since we have negative exponent and to make it as positive exponent, we have to flip the base.

= (-4/5) x (-5/4)²

= (-4/5) x (25/16)

= -5/4

Problem 13 :

By what number should (–3)^–2 be multiplied so that the product may be equal to 9?

Solution :

= (–3)^–2

To change the negative exponent as positive exponent, we have to take the reciprocal 

= 1/(–3)²

= 1/9

To make 1/9 as 9, we have to multiply this 1/9 by 81.

Problem 14 :

By what number should (–12)^–1 be divided so that the quotient may be equal to (–4)^{– 1}?

Solution :

(–12)^–1

Let x be the required number.

(–12)^–1 / x = (–4)^{– 1}?

x = (–12)^–1 / (–4)^{– 1}

= (-1/12)/(-1/4)

= (1/12) x (4/1)

= 1/3

So, the required number is 1/3.

Problem 15 :

Find the value of x :

3² x (-4)² = (-12)^2x

Solution :

3² x (-4)² = (-12)^2x

Since we have same power for both terms in the left side, we can multiply the bases and out one power.

(3 x (-4))² = (-12)^2x

(-12)² = (-12)^2x

Since bases are equal, we can equate the powers.

2 = 2x

x = 2/2

x = 1

So, the value of x is 1.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.