EXPONENTS WITH INTEGER BASES

An integer is a number that can be written without a fractional component. 

Before going to see example problems in this topic, first we have to see what is exponent and what is base.

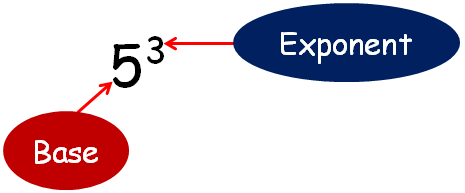
We have the following stuff on exponents of integer bases. 

• Positive base with positive exponent
• Positive base with negative exponent
• Negative base with positive exponent
• Negative base with negative exponent

Positive Base with Positive Exponent

The exponents of a number says, how many times the base has to be multiplied by itself. 

Example 1 :

Evaluate : 

10⁷

Solution :

Base  =  10

Exponent  =  7

Then, 

10⁷ = 10 x 10 x 10 x 10 x 10 x 10 x 10 

10⁷  =  10000000

Example 2 :

Evaluate : 

8²

Solution :

Base  =  8

Exponent  =  2

Then, 

8²  =  8 x 8

  8²  =  64

Positive Base with Negative Exponent

When we have negative exponent for the positive base, first we have to make the exponent as positive. For that, we have to write the reciprocal of the base and change the negative exponent as positive.

Example 3 :

Evaluate : 

3^-2

Solution :

Base  =  3

Exponent  =  -2

Then, 

3^-2  =  (1/3)²

3^-2  =  (1/3) x (1/3)

3^-2  =  1 / 9

Example 4 :

Evaluate : 

4^-3

Solution :

Base  =  4

Exponent  =  -3

Then, 

4^-3  =  (1/4)³

4^-3  =  (1/4) x (1/4) x (1/4) x (1/4)

4^-3  =  1 / 256

Negative Base with Positive Exponent

When we have positive exponent for the negative base, instead of repeating the negative sign, we can follow a simple method to decide whether the answer will be a positive value or negative value. 

• If the exponent is an even number, then the answer will be a positive value.  
• If the exponent is an odd number, then the answer will be a negative value. 

Example 5 :

Evaluate : 

(-7)⁴

Solution :

Base  =  -7

Exponent  =  4

Here, the exponent is 4 which is an even number. So, the answer will be a positive value. 

(-7)⁴  =  7 x 7 x 7 x 7 

(-7)⁴  =  2401

Example 6 :

Evaluate : 

(-2)⁵

Solution :

Base  =  -2

Exponent  =  5

Here, the exponent is 5 which is an odd number. So, the answer will be a negative value. 

(-2)⁵  =  - 2 x 2 x 2 x 2 x 2

(-2)⁵  =  - 32

Negative Base with Negative Exponent

Example 7 :

Evaluate : 

(-3)^-4

Solution :

(-3)^-4  =  (-1/3)⁴

Here, the exponent is 4 which is an even number. So, the answer will be a positive value. 

(-3)^-4  =  (1/3) x (1/3) x (1/3) x (1/3)

(-3)^-4  =  1 / 81

Example 8 :

Evaluate : 

(-6)^-3

Solution :

(-6)^-3  =  (-1/6)³

Here, the exponent is 3 which is an odd number. So, the answer will be a negative value. 

(-6)⁵  =  - (1/6) x (1/6) x (1/6)

(-6)⁵  =  - 1/216

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.