EXPONENTS AND SQUARE ROOTS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Simplify :
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4)
Problem 2 :
Simplify :
(a6 ⋅ b3) / (a2 ⋅ b-3)2
Problem 3 :
If a-1/2 = 5, then find the value of a.
Problem 4 :
If 3x+3 - 3x+2 = k(3x), then solve for k.
Problem 5 :
If x2y3 = 10 and x3y2 = 8, then find the value of x5y5.
Problem 6 :
Simplify the following square root expression :
√40 + √160
Problem 7 :
Simplify the following square root expression :
√27 ⋅ √3
Problem 8 :
Simplify the following square root expression :
(14√117) ÷ (7√52)
Problem 9 :
Simplify the following square root expression :
(√3)3 + √27
Problem 10 :
Rationalize the denominator :
(3 - √3) / √3

Problem 1 :
Simplify :
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4)
Solution :
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a7+2-4 / a2-3+4
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a5 / a3
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a5-3
(a7 ⋅ a2 ⋅ a-4) / (a2 ⋅ a-3 ⋅ a4) = a2
Problem 2 :
Simplify :
(a6 ⋅ b3) / (a2 ⋅ b-3)2
Solution :
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = (a6 ⋅ b3) / [(a2)2 ⋅ (b-3)2]
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = (a6 ⋅ b3) / (a4 ⋅ b-6)
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = a6-4 ⋅ b3+6
(a6 ⋅ b3) / (a2 ⋅ b-3)2 = a2b9
Problem 3 :
If a-1/2 = 5, then find the value of a.
Solution :
a-1/2 = 5
a = 5-2/1
a = 5-2
a = 1/52
a = 1/25
Problem 4 :
If 3x+3 - 3x+2 = k(3x), then solve for k.
Solution :
3x+3 - 3x+2 = k(3x)
Using laws of exponents, we have
3x ⋅ 33 - 3x ⋅ 32 = k(3x)
3x ⋅ 27 - 3x ⋅ 9 = k(3x)
3x(27 - 9) = k(3x)
3x(18) = k(3x)
Divide each side by 3x.
18 = k
So, the value of k is 18.
Problem 5 :
If x2y3 = 10 and x3y2 = 8, then find the value of x5y5.
Solution :
x2y3 = 10 -----(1)
x3y2 = 8 -----(2)
Multiply (1) and (2) :
(1) ⋅ (2) -----> (x2y3) ⋅ (x3y2) = 10 ⋅ 8
x5y5 = 80
So, the value x5y5 is 80.
Problem 6 :
Simplify the following square root expression :
√40 + √160
Solution :
Decompose 40 and 160 into prime factors using synthetic division.
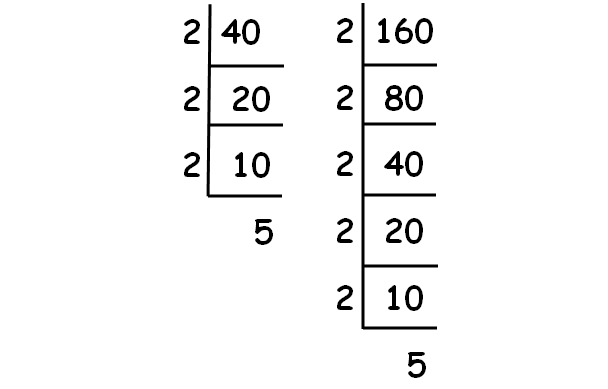
√40 = √(2 ⋅ 2 ⋅ 2 ⋅ 5) = 2√10
√160 = √(2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 5) = 4√10
So, we have
√40 + √160 = 2√10 + 4√10
√40 + √160 = 6√10
Problem 7 :
Simplify the following square root expression :
√27 ⋅ √3
Solution :
√27 ⋅ √3 = √(27 ⋅ 3)
√27 ⋅ √3 = √(3 ⋅ 3 ⋅ 3 ⋅ 3)
√27 ⋅ √3 = 3 ⋅ 3
√27 ⋅ √3 = 9
Problem 8 :
Simplify the following square root expression :
(14√117) ÷ (7√52)
Solution :
Decompose 117 and 52 into prime factors using synthetic division.
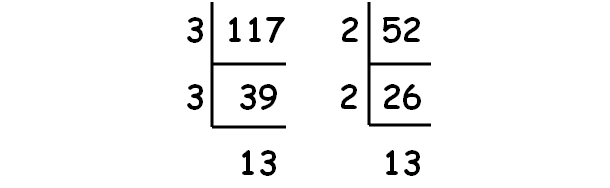
|
√117 = √(3 ⋅ 3 ⋅ 13) √117 = 3√13 |
√52 = √(2 ⋅ 2 ⋅ 13) √52 = 2√13 |
(14√117) ÷ (7√52) = 14(3√13) ÷ 7(2√13)
(14√117) ÷ (7√52) = 42√13 ÷ 14√13
(14√117) ÷ (7√52) = 42√13 / 14√13
(14√117) ÷ (7√52) = 3
Problem 9 :
Simplify the following square root expression :
(√3)3 + √27
Solution :
(√3)3 + √27 = (√3 ⋅ √3 ⋅ √3) + √(3 ⋅ 3 ⋅ 3)
(√3)3 + √27 = (3 ⋅ √3) + 3√3
(√3)3 + √27 = 3√3 + 3√3
(√3)3 + √27 = 6√3
Problem 10 :
Rationalize the denominator :
(3 - √3) / √3
Solution :
To get rid of the radical in denominator, multiply both numerator and denominator by √3.
(3 - √3) / √3 = [(3-√3) ⋅ √3] / (√3 ⋅ √3)
(3 - √3) / √3 = (3√3 - 3) / 3
(3 - √3) / √3 = 3(√3 - 1) / 3
(3 - √3) / √3 = √3 - 1
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com
Recent Articles
-
10 Hard SAT Math Questions (Part - 40)
Dec 18, 25 06:27 PM
10 Hard SAT Math Questions (Part - 40) -
Digital SAT Math Problems and Solutions (Part - 13)
Dec 18, 25 12:26 PM
Digital SAT Math Problems and Solutions (Part - 13) -
90 Degree Clockwise Rotation
Dec 18, 25 09:42 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation

