EXPLORING SOLIDS

Already we know about two-dimensional or flat shapes. In this section, we are going to expand to 3D. All three dimensional shapes are examples of solid figures or solids. 

Polyhedra

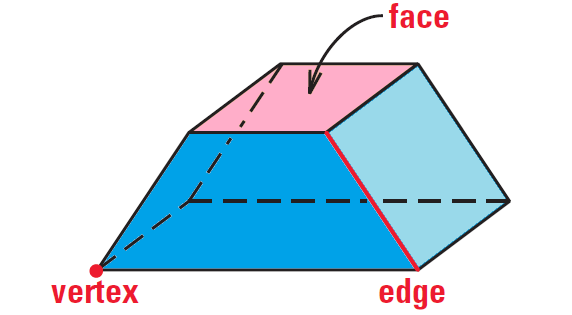
A polyhedron is a solid that is bounded by polygons, called faces that enclose a single region of space. An edge of a polyhedron is a line segment formed by the intersection of two faces. A vertex of a polyhedron is a point where three or more edges meet. The plural of polyhedron is polyhedra, or polyhedrons.

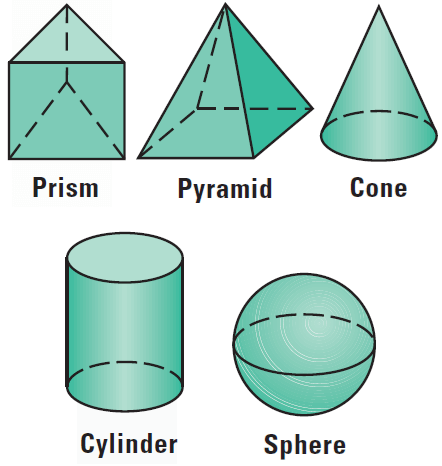
Types of Solids

Of the five solids shown below, the prism and pyramid are polyhedra. The cone, cylinder, and sphere are not polyhedra.

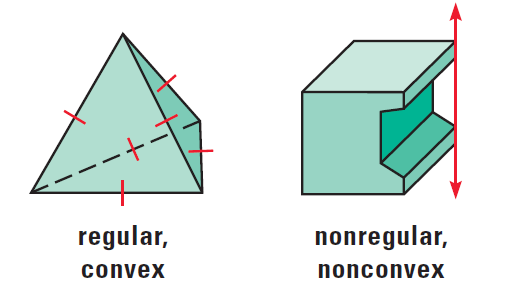
Regular, Convex, Non-regular and Non-convex Polyhedra

A polyhedron is regular, if all of its faces are congruent regular polygons. A polyhedron is convex, if any two points on its surface can be connected by a segment that lies entirely inside or on the polyhedron. If this segment goes outside the polyhedron, then the polyhedron is non-convex, or concave.

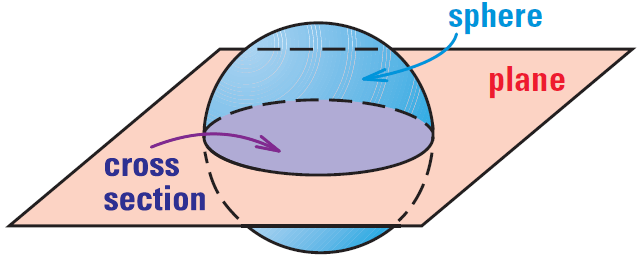
Cross Section of a Solid

Imagine a plane slicing through a solid. The intersection of the plane and the solid is called a cross section. For instance, the diagram shows that the intersection of a plane and a sphere is a circle.

Using Euler's Theorem

There are five regular polyhedra, called Platonic solids, after the Greek mathematician and philosopher Plato. The Platonic solids are a regular tetrahedron (4 faces), a cube (6 faces), a regular octahedron (8 faces), a regular dodecahedron (12 faces), and a regular icosahedron (20 faces).  

Regular Tetrahedron :

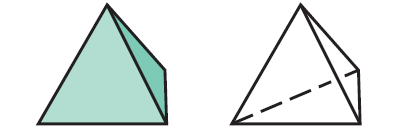
A regular tetrahedron has 4 faces, 4 vertices and 6 edges. 

Cube :

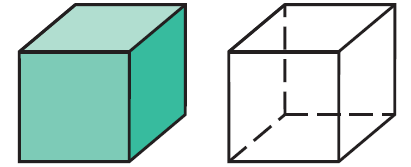
A cube has 6 faces, 8 vertices and 12 edges.  

Regular Octahedron :

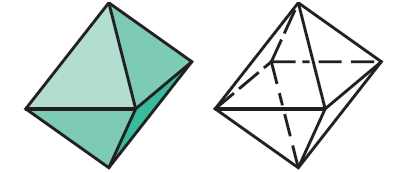
A regular octahedron has 8 faces, 6 vertices and 12 edges. 

Regular Dodecahedron :

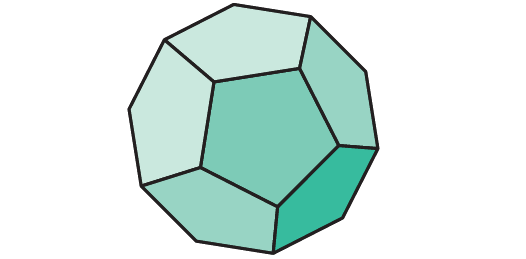
A regular dodecahedron has 12 faces, 20 vertices and 30 edges. 

Regular Icosahedron :

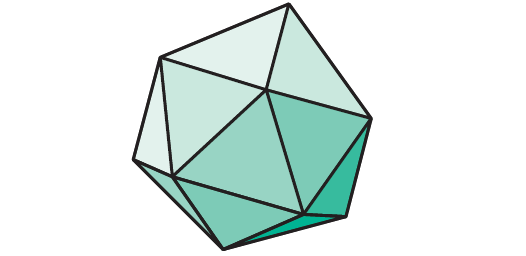
A regular icosahedron has 20 faces, 12 vertices and 30 edges. 

In all the above polyhedra, we can notice that the sum of the number of faces and vertices is two more than the number of edges in the solids above. This result was proved by the Swiss mathematician Leonhard Euler (1707–1783).

Euler's Theorem

The number of faces (F ), vertices (V ), and edges (E ) of a polyhedron are related by the formula

F + V  =  E + 2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.