EXPLORING SOLIDS WORKSHEET

Problem 1 :

Decide whether the solid is a polyhedron. If so, count the number of faces, vertices, and edges of the polyhedron.

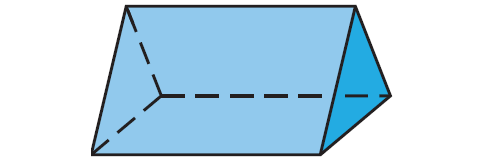
Problem 2 :

Decide whether the solid is a polyhedron. If so, count the number of faces, vertices, and edges of the polyhedron.

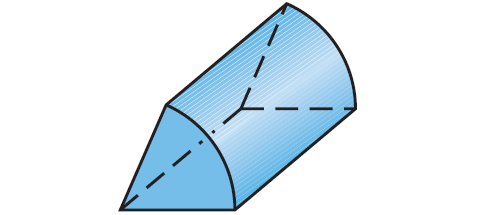
Problem 3 :

Decide whether the solid is a polyhedron. If so, count the number of faces, vertices, and edges of the polyhedron.

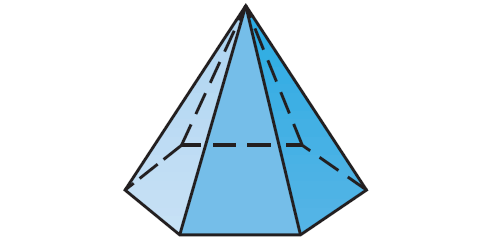
Problem 4 :

Is the octahedron convex ? Is it regular ?

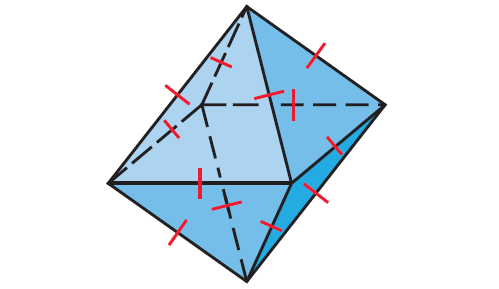
Problem 5 :

Is the octahedron convex ? Is it regular ?

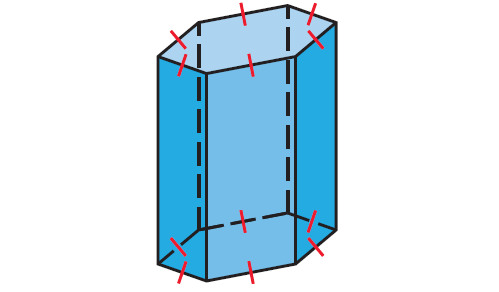
Problem 6 :

Is the octahedron convex ? Is it regular ?

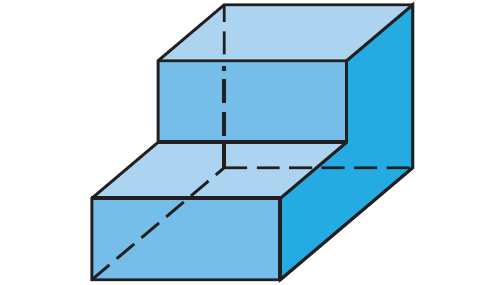
Problem 7 :

Describe the shape formed by the intersection of the plane and the cube.

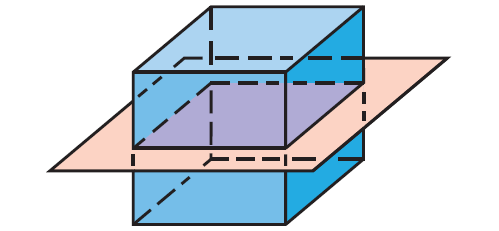
Problem 8 :

Describe the shape formed by the intersection of the plane and the cube.

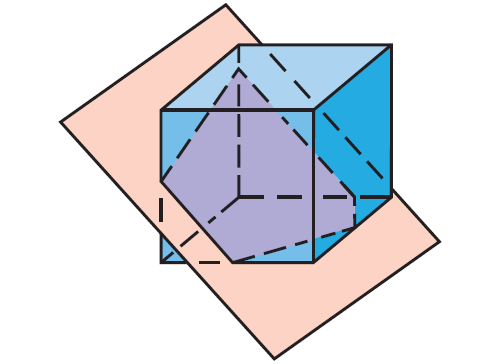
Problem 9 :

Describe the shape formed by the intersection of the plane and the cube.

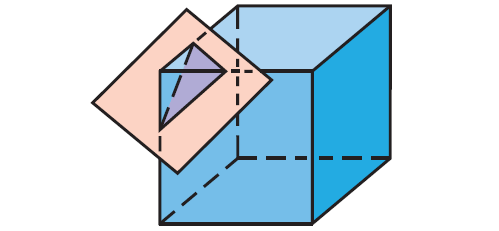
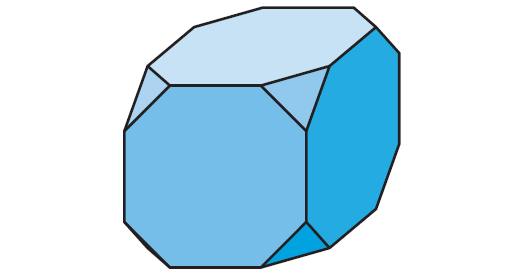
Problem 10 :

The solid shown below has 14 faces; 8 triangles and 6 octagons. How many vertices does the solid have ?

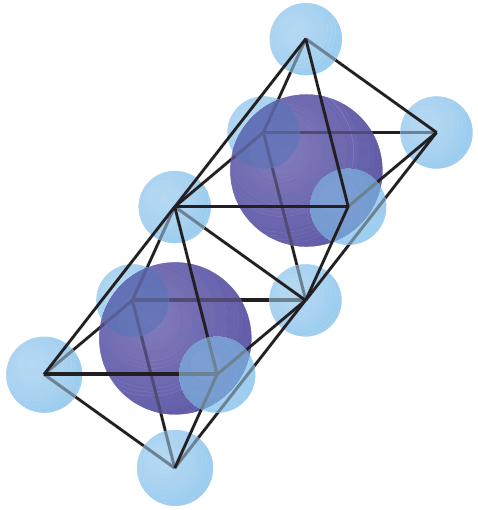
Problem 11 :

In molecules of sodium chloride, commonly known as table salt, chloride atoms are arranged like the vertices of regular octahedrons. In the crystal structure, the molecules share edges. How many sodium chloride molecules share the edges of one sodium chloride molecule ? 

Problem 12 :

A soccer ball resembles a polyhedron with 32 faces ; 20 are regular hexagons and 12 are regular pentagons. How many vertices does this polyhedron have ? 

Answers

Problem 1 :

Decide whether the solid is a polyhedron. If so, count the number of faces, vertices, and edges of the polyhedron.

Answer :

This is a polyhedron. It has 5 faces, 6 vertices, and 9 edges.

Problem 2 : 

Decide whether the solid is a polyhedron. If so, count the number of faces, vertices, and edges of the polyhedron.

Answer :

This is not a polyhedron. Because, some of its faces are not polygons.

Problem 3 : 

Decide whether the solid is a polyhedron. If so, count the number of faces, vertices, and edges of the polyhedron.

Answer :

This is a polyhedron. It has 7 faces, 7 vertices, and 12 edges.

Problem 4 : 

Is the octahedron convex ? Is it regular ?

Answer :

Convex, Regular

Problem 5 : 

Is the octahedron convex ? Is it regular ?

Answer :

Convex, Non-regular

Problem 6 : 

Is the octahedron convex ? Is it regular ?

Answer :

Non-convex, Non-regular

Problem 7 : 

Describe the shape formed by the intersection of the plane and the cube.

Answer :

This cross section is a square.

Problem 8 : 

Describe the shape formed by the intersection of the plane and the cube.

Answer :

This cross section is a pentagon.

Problem 9 : 

Describe the shape formed by the intersection of the plane and the cube.

This cross section is a triangle.

Problem 10 : 

The solid shown below has 14 faces; 8 triangles and 6 octagons. How many vertices does the solid have ?

Answer :

On their own, 8 triangles and 6 octagons have

8(3) + 6(8), or 72 edges

In the solid, each side is shared by exactly two polygons.

So, the number of edges is one half of 72, or 36. 

Use Euler’s Theorem to find the number of vertices.

Write Euler's Theorem :

F + V  =  E + 2

Substitute. 

14 + V  =  36 + 2

14 + V  =  38

Subtract 14 from each side.

V  =  24

So, the solid has 24 vertices. 

Problem 11 : 

In molecules of sodium chloride, commonly known as table salt, chloride atoms are arranged like the vertices of regular octahedrons. In the crystal structure, the molecules share edges. How many sodium chloride molecules share the edges of one sodium chloride molecule ? 

Answer :

To find the number of molecules that share edges with a given molecule, you need to know the number of edges of the molecule.

We know that the molecules are shaped like regular octahedrons. So, they each have 8 faces and 6 vertices. We can use Euler’s Theorem to find the number of edges, as shown below.

Write Euler's Theorem :

F + V  =  E + 2

Substitute. 

8 + 6  =  E + 2

14  =  E + 2

Subtract 2 from each side.

12  =  E

So, 12 other molecules share the edges of the given molecule.

Problem 12 : 

A soccer ball resembles a polyhedron with 32 faces ; 20 are regular hexagons and 12 are regular pentagons. How many vertices does this polyhedron have ? 

Answer :

Each of the 20 hexagons has 6 sides and each of the 12 pentagons has 5 sides. Each edge of the soccer ball is shared by two polygons. Thus, the total number of edges is as follows :

Expression for number of edges : 

E  =  1/2 ⋅ (6 ⋅ 20 + 5 ⋅ 12)

E  =  1/2 ⋅ (120 + 60)

E  =  1/2 ⋅ (180)

E  =  90

Knowing the number of edges, 90, and the number of faces, 32, we can apply Euler’s Theorem to determine the number of vertices.

Write Euler's Theorem :

F + V  =  E + 2

Substitute. 

32 + V  =  90 + 2

32 + V  =  92

Subtract 32 from each side.

V  =  60

So, the polyhedron has 60 vertices.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.