EXPLORING ROTATIONS

A rotation is a transformation that turns a figure around a given point called the center of rotation. The image has the same size and shape as the pre-image.

The triangle XYZ has the following vertices.

X(0, 0), Y(2, 0) and Z(2, 4).

(i)  Trace triangle xyz and the x- and y-axes onto a piece of paper.

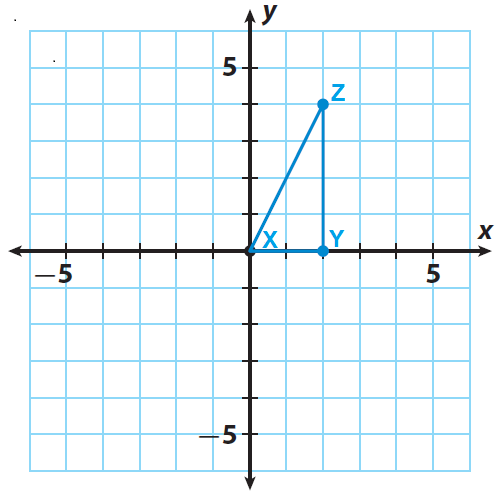
(ii) Rotate your triangle 90° counterclockwise about the origin. The side of the triangle that lies along the x-axis should now lie along the y-axis.

(iii) Sketch the image of the rotation. Label the images of points X, Y, and Z as X', Y', and Z'.

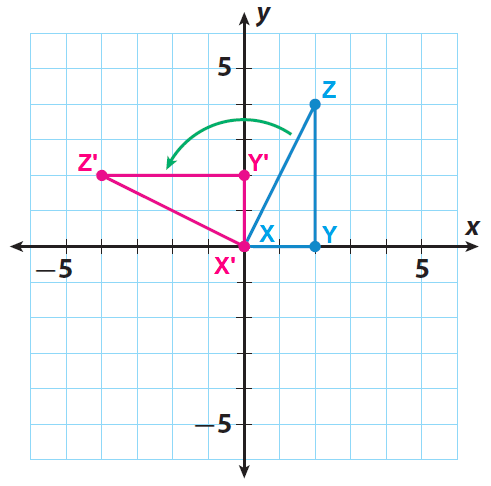
(iv) Write the vertices of the image x'y'z'.

X'(0, 0), Y'(0, 2) and Z'(-4, 2)

(v) Rotate your triangle 90° clockwise about the origin. The side of the triangle that lies along the x-axis should now lie along the y-axis.

(vi) Sketch the image of the rotation. Label the images of points X, Y, and Z as X", Y", and Z".

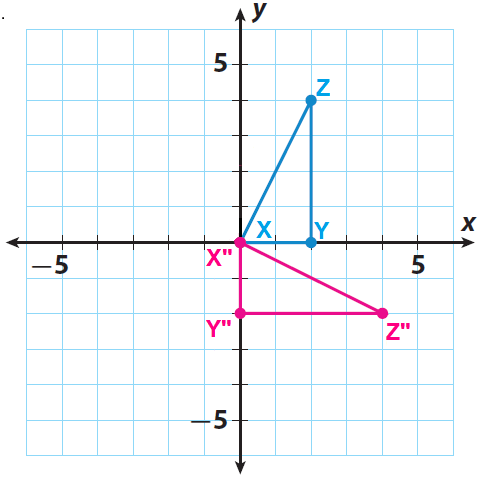
(vii) Write the vertices of the image x"y"z".

X"(0, 0), Y"(0, -2) and Z"(4, -2)

(viii) Based on the rotations done above, write the general rule for 90° counterclockwise rotation about the origin.

X(0, 0) ----> X'(0, 0)

Y(2, 0) ----> Y'(0, 2)

Z(2, 4) ----> Z'(-4, 2)

From the above transformations of vertices, we have the following general rule for 90° counterclockwise rotation.

(ix) Based on the rotations done above, write the general rule for 90° clockwise rotation about the origin.

X(0, 0) ----> X"(0, 0)

Y(2, 0) ----> Y"(0, -2)

Z(2, 4) ----> Z"(4, -2)

From the above transformations of vertices, we have the following general rule for 90° clockwise rotation.

Similarly, we can define general rules for clockwise and counterclockwise rotations of 180° and 270°  about the origin as given below.

Reflect

How are the size and the orientation of the triangle affected by the rotation?

The size stays the same, but the orientation changes in that the triangle is turned or tilted left – what was 'up' is now 'left'.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.