EXPLORING ROTATIONS WORKSHEET

Question 1 :

The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 90° counterclockwise about the origin and write the vertices of the image.

Question 2 :

The triangle XYZ has the following vertices X(0, 0), Y(2, 0) and Z(2, 4). Rotate the triangle XYZ 90° clockwise about the origin and write the vertices of the image.

Question 3 :

Based on the rotation in question 1, write the general rule for 90° counterclockwise rotation about the origin.

Question 4 :

Based on the rotation in question 2, write the general rule for 90° clockwise rotation about the origin.

Question 5 :

How are the size and the orientation of the triangle affected by the rotation?

1. Answer :

Step 1 :

Trace triangle xyz and the x- and y-axes onto a piece of paper.

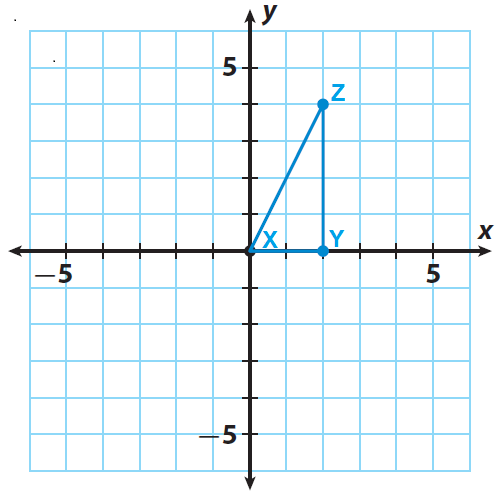
Step 2 :

Rotate your triangle 90° counterclockwise about the origin. The side of the triangle that lies along the x-axis should now lie along the y-axis.

Step 3 :

Sketch the image of the rotation. Label the images of points X, Y, and Z as X', Y', and Z'.

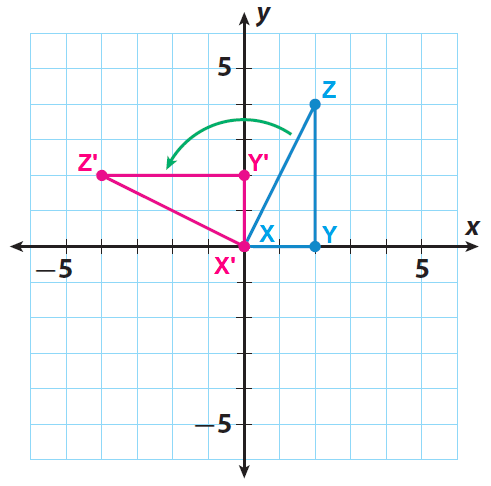
Step 4 :

Write the vertices of the image x'y'z'.

X'(0, 0), Y'(0, 2) and Z'(-4, 2)

2. Answer :

Step 1 :

Trace triangle xyz and the x- and y-axes onto a piece of paper.

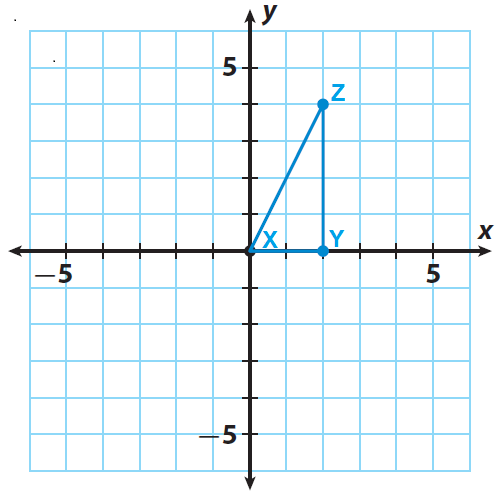
Step 2 :

Rotate your triangle 90° clockwise about the origin. The side of the triangle that lies along the x-axis should now lie along the y-axis.

Step 3 :

Sketch the image of the rotation. Label the images of points X, Y, and Z as X", Y", and Z".

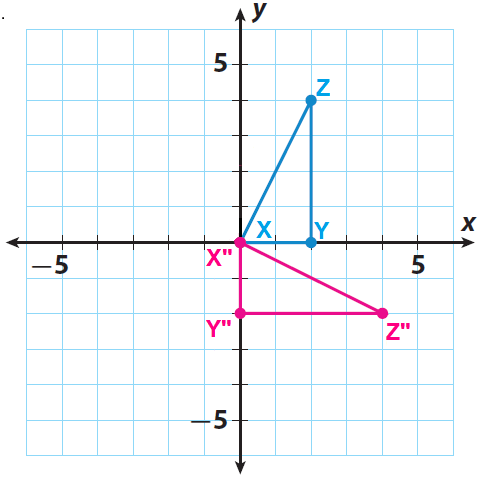
Step 4 :

Write the vertices of the image x"y"z".

X"(0, 0), Y"(0, -2) and Z"(4, -2)

3. Answer :

X(0, 0) ----> X'(0, 0)

Y(2, 0) ----> Y'(0, 2)

Z(2, 4) ----> Z'(-4, 2)

From the above transformations of vertices, we have the following general rule for 90° counterclockwise rotation.

4. Answer :

X(0, 0) ----> X"(0, 0)

Y(2, 0) ----> Y"(0, -2)

Z(2, 4) ----> Z"(4, -2)

From the above transformations of vertices, we have the following general rule for 90° clockwise rotation.

Similarly, we can define general rules for clockwise and counterclockwise rotations about 180°and 270° as given below.

5. Answer :

The size stays the same, but the orientation changes in that the triangle is turned or tilted left – what was 'up' is now 'left'.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.