EXPLORING REFLECTIONS

A reflection is a transformation that flips a figure across a line. The line is called the line of reflection. Each point of the original figure and its corresponding point on the image must be at the same distance from the line of reflection.

The triangle PQR has the following vertices.

P(2, 5), Q(6, 2) and R(2, 2)

(i) Trace triangle PQR and the x- and y-axes onto a piece of paper.

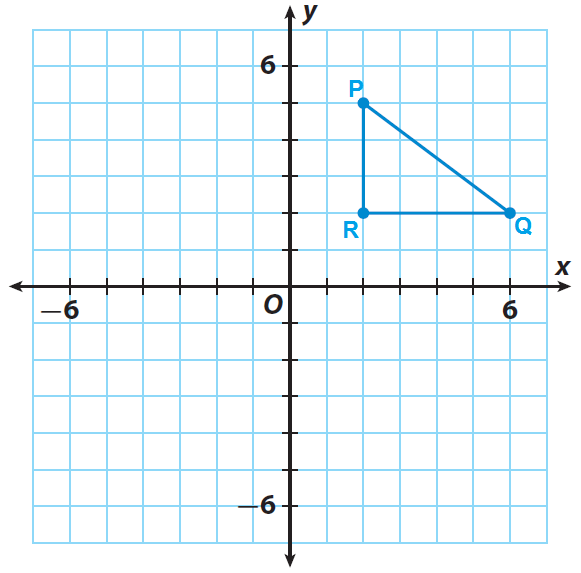
(ii) Fold the paper along the x-axis and trace the image of the triangle on the opposite side of the x-axis. Now, unfold the paper and label the vertices of the image P′, Q′ and R′.

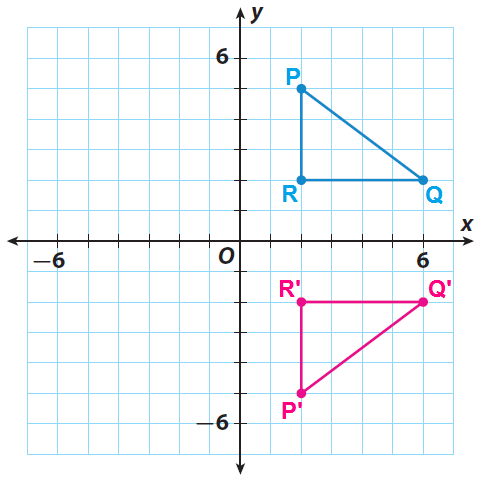
(iii) Since the paper is folded along the x-axis, the line of reflection is x-axis.

(iv) For the original figure, find the perpendicular distance from each point to the line of reflection.

From Point P to the line of reflection = 5 units

From Point Q to the line of reflection = 2 units

From Point R to the line of reflection = 2 units

(v) For the reflected figure, find the perpendicular distance from each point to the line of reflection.

From Point P' to the line of reflection = 5 units

From Point Q' to the line of reflection = 2 units

From Point R' to the line of reflection = 2 units

(vi)  From parts (iv) and (v), it is clear that each point of the original figure PQR and its corresponding point on the image P'Q'R' must be at the same distance from the line of reflection.

(vii)  Fold the paper along the y-axis and trace the image of the triangle on the left side of the y-axis. Now, unfold the paper and label the vertices of the image P", Q" and R".

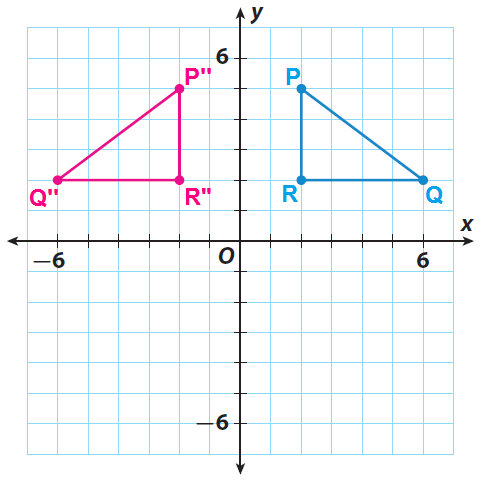
(viii) Since the paper is folded along the y-axis, the line of reflection is y-axis.

(ix) For the original figure, find the perpendicular distance from each point to the line of reflection.

From Point P to the line of reflection = 2 units

From Point Q to the line of reflection = 6 units

From Point R to the line of reflection = 2 units

(x) For the reflected figure, find the perpendicular distance from each point to the line of reflection.

From Point P" to the line of reflection = 2 units

From Point Q" to the line of reflection = 6 units

From Point R" to the line of reflection = 2 units

(xi)  From parts (ix) and (x), it is clear that each point of the original figure PQR and its corresponding point on the image P"Q"R" must be at the same distance from the line of reflection.

Reflect

How does each image in the drawings compare with its pre-image?

Triangle P'Q'R' is triangle P'Q'R' flipped across the x-axis. And triangle P"Q"R" is triangle PQR flipped across the y-axis.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.