EXPLORING RATIOS

A ratio is a comparison of two quantities. It shows how many times as great one quantity is than another.

For example, the ratio of star-shaped beads to moon-shaped beads in a bracelet is 3 to 1. This means that for every 3 star beads, there is 1 moon bead.

The numbers in a ratio are called terms. Suppose that in a pet store there are 5 dogs for every 3 cats. The ratio of dogs to cats is 5 to 3.

The terms of the ratio are 5 and 3. The ratio can also be written as follows.

5 dogs to 3 cats  or   5 to 3   or  5 : 3  or  5/3

A ratio can compare a part to a part, a part to the whole, or the whole to a part.

Exploring Ratios with its Properties

1. Ratio exists only between quantities of the same kind.

2. Quantities to be compared (by division) must be in the same units.

3. The order of the terms in a ratio is important.

4. Both terms of a ratio can be multiplied or divided by the same (non–zero) number. Usually a ratio is expressed in lowest terms (or simplest form).

5. The order of the terms in a ratio is important.

6. To compare two ratios, convert them into equivalent like fractions.

7.  If a quantity increases or decreases in the ratio a : b, then new quantity is  

The fraction by which the original quantity is multiplied to get a new quantity is called the factor multiplying ratio.

8. One ratio is the inverse of another, if their product is 1. Thus a : b is the inverse of b : a and vice–versa.

9. A ratio a : b is said to be of greater inequality if a > b and of less inequality if a < b.

10. The ratio compounded of the two ratios a : b and c : d is ac : bd.

11. A ratio compounded of itself is called its duplicate ratio. 

Thus a² : b² is the duplicate ratio of a : b. Similarly, the triplicate ratio of a : b is a³ : b³.

12. The sub–duplicate ratio of a : b is √a : √b and the sub triplicate ratio of a : b is ³√a : ³√b.

13. If the ratio of two similar quantities can be expressed as a ratio of two integers, the quantities are said to be commensurable; otherwise, they are said to be in-commensurable. 

√3 : √2 cannot be expressed as the ratio of two integers and therefore, √3 and √2 are in-commensurable quantities.

14. Continued Ratio is the relation (or compassion) between the magnitudes of three or more quantities of the same kind. The continued ratio of three similar quantities a, b, c is written as a: b: c.

Examples

Example 1 :

The average age of three boys is 25 years and their ages are in the proportion 3 : 5 : 7. The age of the youngest boy is  

Solution :

From the ratio 3 : 5 : 7, the ages of three boys are

3x, 5x and 7x

Average age of three boys is 25 years (given).

(3x + 5x + 7x) / 3  =  25

15x  =  75

x  =  5

Age of the first boy is 

=  3x  =  3(5)  =  15

Age of the first boy is

=  5x  =  5(5)  =  25

Age of the first boy is 

=  7x  =  7(5)  =  105

So, the age of the youngest boy is 15 years.

Example 2 :

John weighs 56.7 kilograms. If he is going to reduce his weight in the ratio 7 : 6, find his new weight.

Solution :

Original weight of John is 56.7 kg (given).

He is going to reduce his weight in the ratio 7 : 6. 

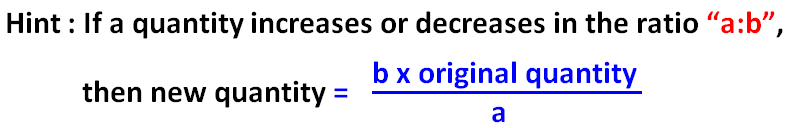
His new weight is 

=  (6 ⋅ 56.7) / 7

=  6 ⋅ 8.1

=  48.6

So, his new weight is 48.6 kg.

Example 3 :

The ratio of the no. of boys to the number of girls in a school of 720 students is 3 : 5. If 18 new girls are admitted in the school, find how many new boys may be admitted so that the ratio of the no. of boys to the no. of girls may change to 2 : 3.

Solution :

Sum of the terms in the given ratio is

=  3 + 5

=  8 

So, no. of boys in the school  is 

=  720 ⋅ (3/8)

=  270 

Number of girls in the school is

=  720 ⋅ (5/8)

=  450

Let x be the no. of new boys admitted in the school. 

Number of new girls admitted is 18 (given). 

After the above new admissions, 

no. of boys in the school  =  270 + x

no. of girls in the school  =  450 + 18  =  468

The ratio after the new admission is 2 : 3 (given).

So,

(270 + x) : 468  =  2 : 3

3(270 + x)  =  468 ⋅ 2

810 + 3x  =  936

3x  =  126

x  =  42

So, the number of new boys admitted in the school is 42.

Example 4 :

The monthly incomes of two persons are in the ratio 4 : 5 and their monthly expenditures are in the ratio 7 : 9. If each saves $50 per month, find the monthly income of the second person. 

Solution :

From the given ratio of incomes 4 : 5, 

income of the 1st person  =  4x 

income of the 2nd person  =  5x

(Expenditure  =  Income - Savings)

Then, expenditure of the 1st person is 

=  4x - 50

Expenditure of the 2nd person is

=  5x - 50

Expenditure ratio is 7 : 9 (given).

So,

(4x - 50) : (5x - 50)  =  7 : 9 

9(4x - 50)  =  7(5x - 50) 

36x - 450  =  35x - 350  

x  =  100 

Then, income of the second person is

 =  5x

=  5(100)

=  500.

So, income of the second person is $500.

Example 5 :

If the angles of a triangle are in the ratio 2 : 7 : 11, then find the angles.

Solution :

From the ratio 2 : 7 : 11,

the three angles are 2x, 7x, 11x

In any triangle, sum of the angles is 180°

So,

2x + 7x + 11x  =  180°

20x  =  180°

x  =  9°

Then, the first angle is 

=  2x  =  2(9°)  = 18°

The second angle is

=  7x  =  7(9°)  =  63°

The third angle is

=  11x  =  11(9°)  =  99°

So, the angles of the triangle are (18°, 63°, 99°).

Example 6 :

In a business, if A can earn $7500 in 2.5 years, find the unit rate of his earning per month. 

Solution : 

Given : Earning in 2.5 years  =  $7500.

1 year  =  12 months

2.5 years  =  2.5 x 12  =  30 months

Then, earning in 30 months is $7500.

Therefore, earning in 1 month is

=  7500 / 30

=  $250

So, the unit rate of his earning per month is $250.

Example 7 :

If David can prepare 2 gallons of juice in 4 days, how many  cups of juice can he prepare per day ? 

Solution : 

No of gallons of juice prepared in 4 days  =  2 gallons

1 gallon  =  16 cups

So, no. of cups of juice prepared in 4 days

=  2 ⋅ 16

=  32 cups

Therefore, David can prepare 32 cups of juice in 4 days. 

Then, no. of cups of juice prepared in 1 day is

=  32/4

=  8

So, David can prepare 8 cups of juice in 1 day. 

Example 8 :

If John can cover 360 miles in 3 hours, find the number of miles covered by John in 1 minute.  

Solution : 

No. of miles covered in 3 hours is 360.

Then, no. of miles covered in 1 hour is

=  360/3

=  180

1 hour  =  60 minutes

So, no. of miles covered in 60 minutes is 180.

Then, no. of miles covered 1 minute is

=  180/60

=  3

So, John can cover 3 miles in 1 minute. 

Example 9 : 

Shanel walks 2/5 of a mile every 1/7 hour. Express her speed as a unit rate in miles per hour. 

Solution : 

Given : Shanel walks 2/5 of a mile every 1/7 hour.

We know the formula for speed.

That is,  

Speed  =  Distance / time

Speed  =  (2/5)  /  (1/7)

Speed  =  (2/5) ⋅ (7/1)

Speed  =  14 / 5

Speed  =  2.8 miles per hour. 

So, the speed of Shanel is 2.8 miles per hour.

Example 10 : 

Declan use 2/35 of a gallon of gas for every 4/5 of a mile that he drives. At this rate, how many miles can he drive on one gallon of gas ? 

Solution : 

Given : In 2/35 of a gallon of gas, 4/5 of a mile is traveled.

Then, in  1 gallon of gas is 

=  (4/5) ⋅ (35/2) miles traveled 

=  14 miles traveled

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.