EXPLORING GRAPHS OF QUADRATIC FUNCTIONS

The graph of any quadratic function will be a parabola.  

The general form of a quadratic function is 

y  =  ax² + bx + c

To explore the graphs of quadratic functions, we have to be aware of the following stuff. 

(i)  Open upward or open downward parabola

(ii)  Vertex

(iii)  x - intercepts

(x - intercepts are nothing but the points where the curve cuts x - axis)

(iv) y - intercept 

(y - intercepts are nothing but the points where the curve cuts y - axis)

Let us see the above stuff in detail. 

(i) Open upward or downward :

y  =  ax² + bx + c

If the leading coefficient or the sign of 'a' is positive, the parabola is open upward and 'a' is negative, the parabola is open downward.  

(ii) Vertex :

To find the vertex of the parabola which is given by the quadratic function y  =  ax² + bx + c, we have to find the value x using the formula given below. 

x  =  -b / 2a

And the vertex is 

[-b/2a, y(-b/2a)]

(iii) X - intercepts :

To know the x - intercepts, we have to plug y = 0 in

y  =  ax² + bx + c

and find the values of x.

Note : 

If the values of x are imaginary, the curve will not intersect x - axis. 

(iii) Y - intercept :

To know the y - intercept, we have to plug x = 0 in

y  =  ax² + bx + c

and find the value of y.

Based on the results which we get from the above four points, we have to sketch parabola. 

Example 1 : 

Graph the quadratic equation that is given below. 

x² + 5x + 6 = 0

Solution : 

Let y = x² + 5x + 6

Step 1 :

In the given quadratic function, since the leading coefficient (x²) is positive, the parabola will be open upward. 

Step 2 :

When the given quadratic function is compared to

y  =  ax² + bx + c,

we get 

a  =  1

b  =  5

c  =  6

x coordinate of the vertex is 

=  -b / 2a

=  -5 / 2(1)

=  -5 / 2

=  -2.5

y coordinate of the vertex is 

=  y(-2.5)

=  (-2.5)² + 5(-2.5) + 6

=  6.25 - 12.5 + 6

=  -0.25

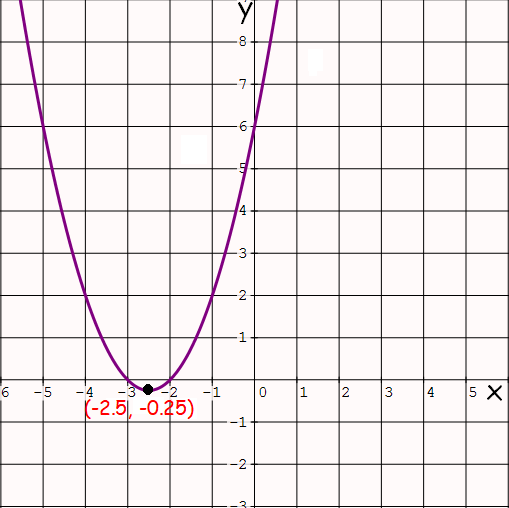
So, the vertex is (-2.5, -0.25).

Step 3 :

To know x - intercept, we have to substitute y = 0 in the given quadratic function. 

Then, we have

0  =  x² + 5x + 6   or   x² + 5x + 6  =  0

(x + 2)(x + 3) = 0

x + 2 = 0 or x + 3 = 0 

x  =  -2  or  x  =  -3

Therefore, the parabola cuts x - axis at

x  =  -2  and  x  =  -3

Step 4 : 

To know y - intercept, we have to substitute x = 0 in the given quadratic function. 

Then, we have

y = (0)² + 5(0) + 6

y  =  6

Therefore, the parabola cuts y - axis at y = 6.

Now, let us sketch the parabola. 

Example 2 : 

Graph the quadratic equation that is given below. 

-2x² + 5x - 7 = 0

Solution : 

Let y = -2x² + 5x - 7

Step 1 :

In the given quadratic function, since the leading coefficient (x²) is negative, the parabola will be open downward. 

Step 2 :

When the given quadratic function is compared to

y  =  ax² + bx + c,

we get 

a  =  -2

b  =  5

c  =  -7

x coordinate of the vertex is 

=  -b / 2a

=  -5 / 2(-2)

=  -5 / (-4)

=  1.25

y coordinate of the vertex is 

=  y(1.25)

=  -2(1.25)² + 5(1.25) - 7

=  -3.125 + 6.25 - 7

=  -3.875

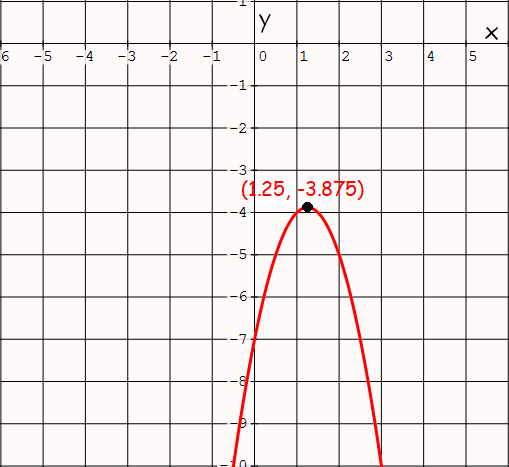
So, the vertex is (1.25, -3.875).

Step 3 :

To know x - intercept, we have to plug y = 0 in the given quadratic function. 

Then, we have

0  =  -2x² + 5x -7   or   -2x² + 5x - 7  =  0

The above quadratic equation can not be solved using factoring.

So let us try to solve the equation using quadratic formula as given below

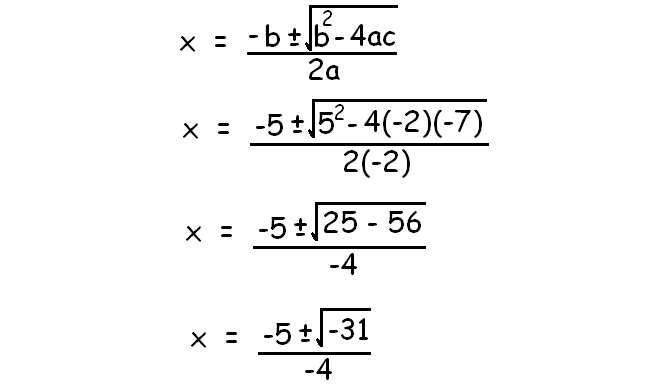
Clearly, the two values of x are imaginary.

Therefore, the parabola does not cut x - axis.

Step 4 : 

To know y - intercept, we have to substitute x = 0 in the given quadratic function. 

Then, we have

y  =  -2(0)² + 5(0) - 7

y  =  -7

Therefore, the parabola cuts y - axis at y = -7.

Now, let us sketch the parabola. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.