EXPLORING DILATIONS ON THE COORDINATE PLANE

In this section,  we will explore how the coordinates of a figure on a coordinate plane are affected by a dilation.

A dilation is a transformation that moves each point on the original figure along a straight line drawn from a fixed point. The point is called the point of dilation and the distance moved is determined by the scale factor used.

Dilations produce figures that are the same shape as the original, but not the same size.

When the scale factor is greater than one, the dilation is called an enlargement.

When the scale factor is less than one, the dilation is called a reduction.

The toy models given below are scaled-down replicas of the Saturn V rocket that powered the moon flights. Each replica is a transformation called a dilation.

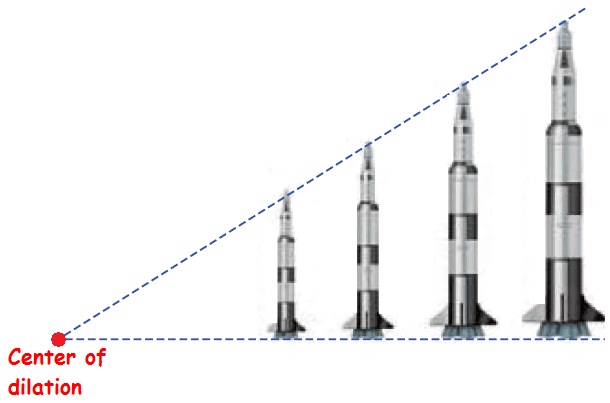
Unlike the other transformations we have studied — translations, rotations, and reflections — dilations change the size (but not the shape) of a figure.

Exploring Dilations on the Coordinate Plane

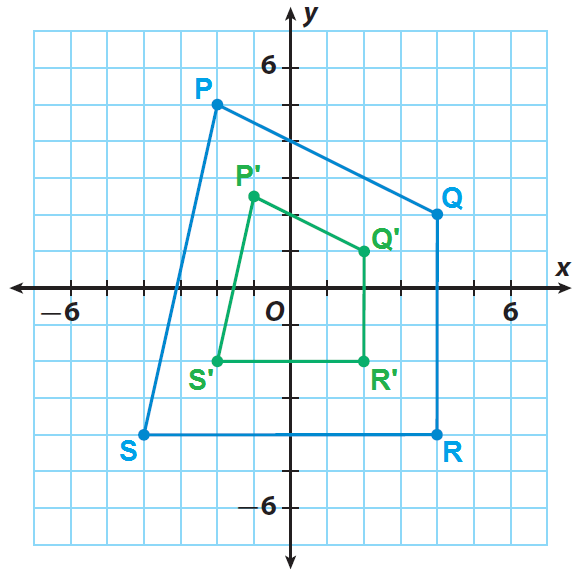
Quadrilateral P'Q'R'S' is a dilation of quadrilateral PQRS. Origin "O" is the center of dilation.

Step 1 :

Record the x- and y-coordinates of the points in quadrilateral PQRS and quadrilateral P'Q'R'S'.

Step 2 :

Find the ratios of the x-coordinates and the y-coordinates of the quadrilaterals P'Q'R'S' and PQRS.

Step 3 :

Write a conjecture about the ratios of the coordinates of a dilation image to the coordinates of the original figure.

All the ratios are equal and it is 0.5. So, the distances are proportional.

Step 4 :

How is the relationship between quadrilateral P′Q′R′S′ and quadrilateral PQRS different?

Quadrilateral P'Q'R'S' is smaller than quadrilateral PQRS.

Step 5 :

Measure the corresponding angles and describe your results.

The corresponding angles are congruent.

PQRS and P'Q'R'S' are similar quadrilaterals.

Since the corresponding angles are congruent, it is clear that the dilations change size but not the shape.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.