EXAMPLES OF ADDING AND SUBTRACTING RATIONAL EXPRESSIONS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Simplify :
(x + 2)/(x + 3) + (x - 1)/(x + 3)
Solution :
Because the denominators are same, we have to take the denominator once and combine the numerators.
= (x + 2 + x - 1) / (x + 3)
= (2x + 1) / (x + 3)
Example 2 :
Simplify :
[(x + 1) / (x - 1)2] + [1 / (x + 1)]
Solution :
Here, the denominators are not same.
So, we have to find the least common multiple of the denominators.
Least common multiple of the denominators is
(x - 1)2(x + 1)
Then,
= [(x + 1)(x + 1)/(x + 1)(x - 1)2] + [(x - 1)2/(x + 1)(x -1)2]
= [(x + 1)2/(x + 1)(x - 1)2] + [(x - 1)2/(x + 1)(x -1)2]
= [(x + 1)2+ (x - 1)2] / (x + 1)(x - 1)2
= [x2 + 2x + 1 + x2 - 2x + 1] / (x + 1)(x - 1)2
= (2x2 + 2) / (x + 1)(x - 1)2
Example 3 :
Simplify
[x3/(x - 2)] + [8/(2 - x)]
Solution :
Here, the denominators are not same. But, we can do a small adjustment and make denominator same as shown below.
= (x3 + 8)/(x - 2)] - 8/(x - 2)
Now, the denominators is same. So, we have to take the denominator once and combine the numerators.
= [x3/(x - 2)] - [8/(x - 2)]
= (x3 - 8) / (x - 2)
Use algebraic identity a3 - b3 = (a - b)(a2 + ab + b2) to factor (x3 - 8).
= (x - 2)(x2 + 2x + 4) / (x - 2)
= x2 + 2 x + 4
Example 4 :
Simplify
(x + 2)/(x2 + 3x + 2)] + (x - 3)/(x2 - 2x - 3)
Solution :
x2 + 3 x + 2 = (x + 1)(x + 2)
x2 - 2 x - 3 = (x - 3)(x + 1)
Then,
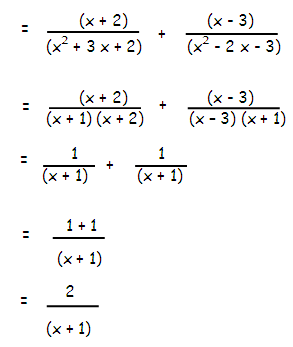
Example 5 :
Simplify
[(x2 - x - 6)/(x2 - 9)] + [(x2 + 2x - 24)/(x2 - x - 12)]
Solution :
= [(x2 - x - 6)/(x2 - 9)] + [(x2 + 2x - 24)/(x2 - x - 12)]
(x2 - x - 6) = (x - 3)(x + 2)
By comparing (x2 - 9) with the algebraic identity
(a2 - b2) = (a + b)(a - b)
we get,
(x2 - 32) = (x + 3)(x - 3)
(x2 + 2 x - 24) = (x + 6) (x - 4)
(x2 - x - 12) = (x - 4) (x + 3)
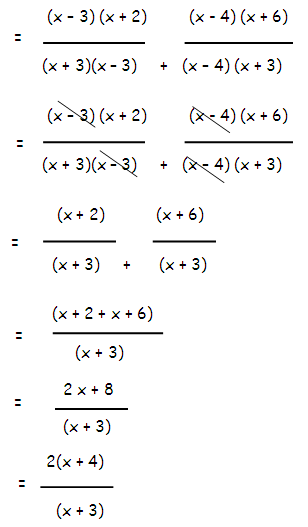
Example 6 :
Simplify
[(2x2-5x+3)/(x2-3x+2)] - [(2x2-7x-4)/(2x2 - 3x - 2)]
Solution :
= [(2x2-5x+3)/(x2-3x+2)] - [(2x2-7x-4)/(2x2 - 3x - 2)]
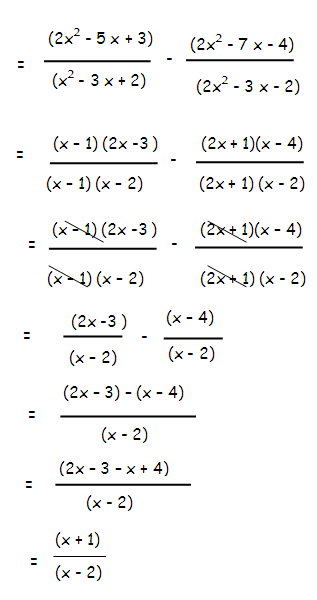
Example 7 :
Simplify
[(x2-4)/(x2+6x+8)]-[(x2-11x+30)/(x2-x - 20)]
Solution :
= [(x2-4)/(x2+6x+8)] - [(x2-11x+30)/(x2-x - 20)]
(x2 - 22) = (x + 2) (x - 2)
(x2+ 6x + 8) = (x + 2) (x + 4)
(x2- 11x + 30) = (x - 6) (x - 5)
(x2- x - 20) = (x - 5) (x + 4)
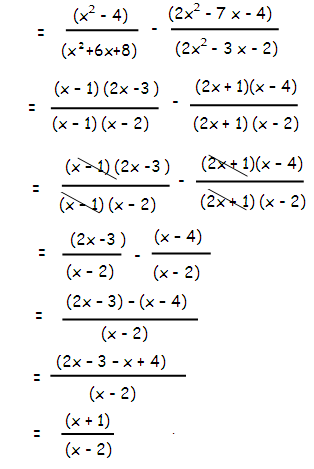
Example 8 :
Simplify
[(2x + 5)/(x + 1)] + [(x2 + 1)/(x2 - 1)] - [(3x - 2)/(x - 1)]
Solution :
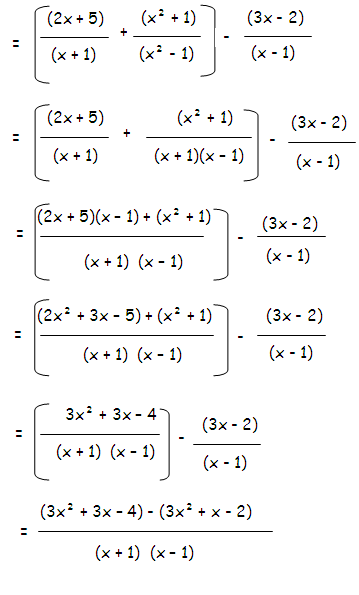
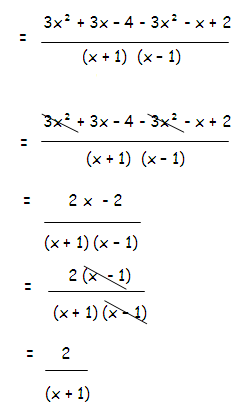
Example 9 :
Simplify
[1/(x2+3x+2)] + [1/(x2+5x+6)] - [2/(x2+4x+3)]
Solution :
(x2 + 3x + 2) = (x + 1) (x + 2)
(x2 + 5x + 6) = (x + 2)(x + 3)
(x2 + 4x + 3) = (x + 3) (x + 1)
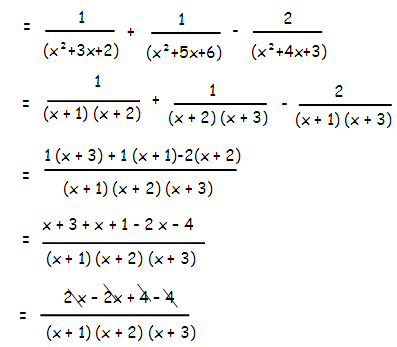
= 0
Example 10 :
Which rational expression should be added to
(x3 - 1)/(x2 + 2) to get (3x3 + 2x2 + 4)/(x2 + 2) ?
Solution :
let the required rational expression be p(x)
[(x3 - 1)/(x2 + 2)] + p(x) = (3x3 + 2x2 + 4)/(x2 + 2)
p(x) = [(3x3 + 2x2 + 4)/(x2 + 2)] - [(x3 - 1)/(x2 + 2)]
Since the denominators are same, we may write only one denominator and combine the numerators.
= [(3x3 + 2x2 + 4) - (x3 - 1)]/(x2 + 2)]
= (3x3 - x3 + 2x2 + 4 + 1)/(x2 + 2)
= (2x3 + 2x2 + 5)/(x2 + 2)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 2)
Feb 19, 26 07:14 PM
Digital SAT Math Problems and Solutions (Part - 2) -
Tricky SAT Math Problems Solved Easily
Feb 19, 26 09:11 AM
Tricky SAT Math Problems Solved Easily -
Digital SAT Math Problems and Solutions (Part - 1)
Feb 18, 26 03:01 AM
Digital SAT Math Problems and Solutions (Part - 1)