EXAMPLE PROBLEMS ON FORMULA BY INDUCTION

Example 1 :

Consider the pattern :

Find the number of matchsticks M required to make the

(a)  1^st, 2^nd and 3^rd figures

(b)  4^th and 5^th figures

(c)  10^th figure

(d)  n^th figure

Solution :

(a)  Number of matchsticks in 1^st figure = 3.

Number of matchsticks in 2^nd figure = 5.

Number of matchsticks in 3^rd figure = 7.

(b)  By observing the above sequence, it is very clear that every element is 2 more than the preceding. By continuing this way, we get

Number of matchsticks in 4^th figure = 7 + 2 = 9.

Number of matchsticks in 5^th figure = 9 + 2 = 11.

(c)  10^th figure

Number of match sticks in the n^th figure = 2n + 1.

If n = 10

number of match sticks in 10^th figure = 2(10) + 1

number of match sticks in 10^th figure = 21

(d)  n^th figure

Number of match sticks in n^th figure = 2n + 1

Example 2 :

Consider the pattern :

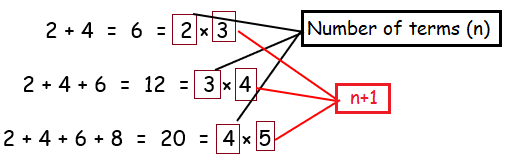
2 + 4 = 6 = 2 × 3

2 + 4 + 6 = 12 = 3 × 4

2 + 4 + 6 + 8 = 20 = 4 × 5

2 terms in the first serious

a) Continue the pattern for 3 more cases.

b) Use a predict a formula for 2 + 4 + 6 + 8 +……+ 2n

c) Use a predict a formula for 1 + 2 + 3 + 4 +……+ n

d) what is the sum of the first 200 positive integers ?

Solution :

By observing the serious above,

(a)  By continuing the pattern, we get

(i) 2 + 4 + 6 + 8 + 10 = 5(5 + 1) = 30

(ii) 2 + 4 + 6 + 8 + 10 + 12 = 6(6 + 1) = 42

(ii) 2 + 4 + 6 + 8 + 10 + 12 + 14 = 7(7 + 1) = 56

b) Use a predict a formula for 2 + 4 + 6 + 8 +……+ 2n.

From (a), it is clear the sum of the series

= number of terms (number of terms + 1)

Since we have n terms

Sum of the series = n(n + 1)

(c) For example,

So, the required formula is n(n + 1)/2.

(d)  Sum of 200 positive integers :

= 200(200 + 1)/2

= 100(201)

= 20100

Example 3 :

For the following match stick pattern, find the number of matches M required to make

(a)  4^th and 5^th figures

(b)  20^th figure

(c)  n^th figure

Solution :

(a)  Number of match sticks in 1^st figure = 7.

nmber of match sticks in 2^nd figure = 7 + 5 = 12

number of match sticks in 3^rd figure = 12 + 5 = 17

number of match sticks in 4^th figure = 17 + 5 = 22

number of match sticks in 5^th figure = 22 + 5 = 27

number of match sticks  =  multiple of 5 + 2

So, the formula is 5n + 2.

(b) Number of match sticks in 20^th figure = 5(20) + 2.

= 100+2

= 102

(c) The required formula is 5n + 2.

Example 4 :

Consider the following pattern,

1 = 1 = 1²

1 + 3 = 4 = 2²

1 + 3 + 5 = 9 = 3²

(a) Continue the pattern for 3 more cases.

(b) Predict the value of 1 + 3 + 5 + 7 +........+ 99.

(c) The 1^st odd number is 1.

The 2^nd odd number is 3.

The 3^rd odd number is 5.

What is the n^th odd number ?

Solution :

(a)

(i) 1 + 3 + 5 + 7 = 16 = 4²

(ii) 1 + 3 + 5 + 7 + 9 = 25 = 5²

(iii) 1 + 3 + 5 + 7 + 9 + 11 = 36 = 6²

n number of terms in each case

(b) Number of terms from 1 to 100 is 100.

Number of odd terms from 1 to 99 is 50.

= 50²

= 2500

(c) Each terms are odd numbers.

Formula = 2n - 1

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.