EXAMPLE PROBLEMS ON BASIC PROPORTIONALITY THEOREM
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Basic Proportionality Theorem :
If a straight line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
Example 1 :
In a triangle ABC,D and E are points on the sides AB and AC respectively such that DE is parallel to BC.
(i) If AD = 6 cm, DB = 9 cm and AE = 8 cm, then find AC.
Solution :
In the given triangle ABC the sides DE is parallel to the side BC. By using “Thales theorem”, we get
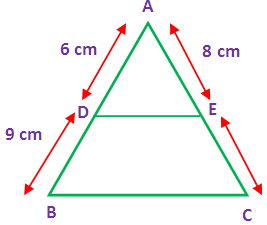
AD/DB = AE/EC
6/9 = 8/EC
EC = (9 ⋅ 8)/6
EC = (3 ⋅ 4)
EC = 12 cm
Example 2 :
In triangle ABC, if AD = 8 cm, AB = 12 cm and AE = 12 cm, then find CE.
Solution :
In the given triangle ABC the sides DE is parallel to the side BC. By using “Thales theorem”, we get
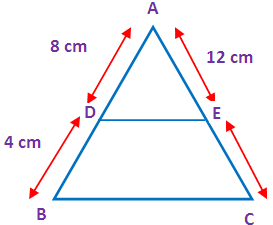
AD/DB = AE/EC
AB = AD + DB
12 = 8 + DB
DB = 4 cm
AD/DB = AE/EC
8/4 = 12/EC
EC = (12 ⋅ 4)/8
EC = 48/8
EC = 6 cm
Example 3 :
In triangle ABC, if AD = 4 x – 3, BD = 3 x – 1, AE = 8 x – 7 and EC = 5 x – 3, then find the value of x.
Solution :
In the given triangle ABC the sides DE is parallel to the side BC. By using “Thales theorem”, we get
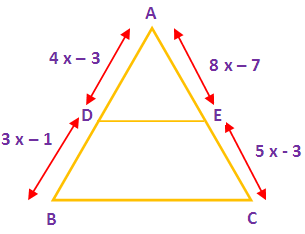
AD/DB = AE/EC
(4x – 3)/(3x – 1) = (8x – 7)/(5x – 3)
(4x – 3)(5x – 3) = (8x – 7)(3x – 1)
20x2 – 12x – 15 x + 9 = 24x2 – 8x – 21x + 7
20x2 – 24x + 9 = 8x2 – 29x + 7
20x2 - 24x2 – 27x + 29x + 9 – 7 = 0
-4x2 + 2 x + 2 = 0
Multiply by -2.
2x2 – x - 1 = 0
(x – 1)(2 x + 1) = 0
|
x - 1 = 0 x = 1 |
2x + 1 = 0 2x = -1 x = -1/2 |
So the value of x is 1.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 18, 26 06:52 PM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
