EXAMPLE PROBLEMS IN DIFFERENTIATION USING CHAIN RULE

Question 1 :

Differentiate y = (1 + cos²x)⁶

Solution :

u  =  1 + cos²x

Differentiate the function "u" with respect to "x"

du/dx  =  0 + 2 cos x (-sin x)  ==>  -2 sin x cos x

du/dx  =  - sin 2x

y = u⁶ 

Differentiate the function "y" with respect to "x"

dy/dx  =  6u⁵ (du/dx)

  =  6(1 + cos²x)⁵ (-sin 2x)

  =  -6 sin 2x (1 + cos²x)⁵

Question 2 :

Differentiate y = e^3x/(1 + e^x)

Solution :

u  =  e^3x  ==>  u'  =  3e^3x

v  =  1 + e^x  ==>  v'  =  e^x

dy/dx  =  [(1 + e^x) (3e^3x) - e^3x (e^x)]/(1 + e^x)²

dy/dx  =  [3e^3x + 3e^4x - e^4x]/(1 + e^x)²

dy/dx  =  [3e^3x + 2e^4x]/(1 + e^x)²

Question 3 :

Differentiate y = √(x+√x)

Solution :

y = √(x+√x)

y² = x + √x

2y (dy/dx)  =  1 + 1/2√x

dy/dx  =  (1/2√(x+√x)) (1 + (1/2√x))

dy/dx  =  (1/2√(x+√x)) (2√x + 1)/2√x)

dy/dx  =  (2√x + 1)/4√x(√(x+√x))

Question 4 :

Differentiate y = e^{xcos x}

Solution :

 y = e^{xcos x}

Let u  =  x cos x

du/dx  =  x (-sinx ) + cos x (1)

du/dx  =  - x sin x + cos x 

y = e^u

dy/dx  =  e^u (du/dx)

dy/dx  =  e^{x cos x} (- x sin x + cos x)

Question 5 :

Differentiate the following

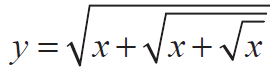
Solution :

y²  =  x + √(x +√x)

2y (dy/dx)  =  1 + 1/2√(x +√x))

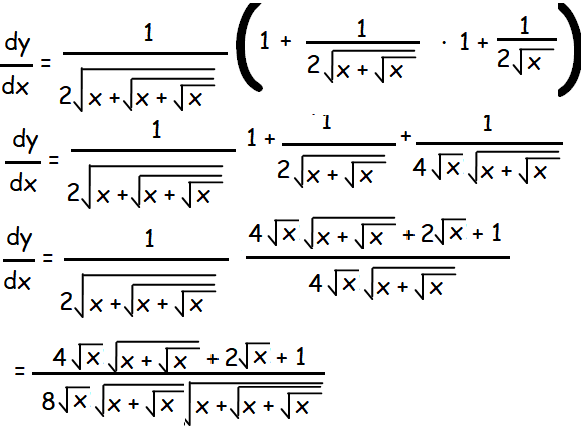
Question 6 :

Differentiate y = sin (tan (√sin x))

Solution :

dy/dx  =  cos (tan (√sin x)) sec² (√sin x) (1/2√sin x) cos x

dy/dx  =  [cos (tan (√sin x)) sec² (√sin x) cos x]/2√sin x

Question 7 :

Differentiate y = sin^-1[(1 - x²)/ (1 + x²)]

Solution :

y = sin^-1[(1 - x²)/ (1 + x²)]

Let u  =  (1 - x²)/(1 + x²)

du/dx  =  [(1 + x²)(-2x) - (1 - x²)(2x)]/(1 + x²)²

=  (-2x - 2x³ - 2x + 2x³) /(1 + x²)²

du/dx  =  -4x /(1 + x²)²

y = sin^-1u

dy/dx  = 1/√(1 - u²) (du/dx)

= 1/√(1 -  ((1 - x²)/(1 + x²))²) [-4x /(1 + x²)²]

=  (1 + x²)/√(1 + x⁴ + 2x² - 1 + 2x² - x⁴)[-4x /(1 + x²)²]

=  ((1 + x²)/2x)[-4x /(1 + x²)²]

dy/dx  =  -2/(1 + x²)

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.