EXAMINING LINEAR RELATIONSHIPS

Recall that a proportional relationship is a relationship between two quantities in which the ratio of one quantity to the other quantity is constant.

The graph of a proportional relationship is a line through the origin.

When ratios between quantities are not constant, a relationship may be linear but not proportional and the graph does not pass through the origin.

Example :

The entrance fee for Mountain World theme park is $20. Visitors purchase additional $2 tickets for rides, games, and food. The equation y = 2x + 20 gives the total cost, y, to visit the park, including purchasing x tickets. 

Explain why the relationship between number of tickets and total cost is not proportional.

Solution :

Step 1 :

Choose several values for x that make sense in context.

x  =  1, 2, 3, 4

Step 2 :

Use the equation y = 2x + 20 to find y for each value of x.

x  =  1 :

y  =  2(1) + 20

y  =  2 + 20

y  =  22

x  =  2 :

y  =  2(2) + 20

y  =  4 + 20

y  =  24

x  =  3 :

y  =  2(3) + 20

y  =  6 + 20

y  =  26

x  =  4 :

y  =  2(4) + 20

y  =  8 + 20

y  =  28

Step 3 :

Let us list out the values of y for the corresponding values of x using a table.

Step 4 :

Plot the ordered pairs from the table. Describe the shape of the graph.

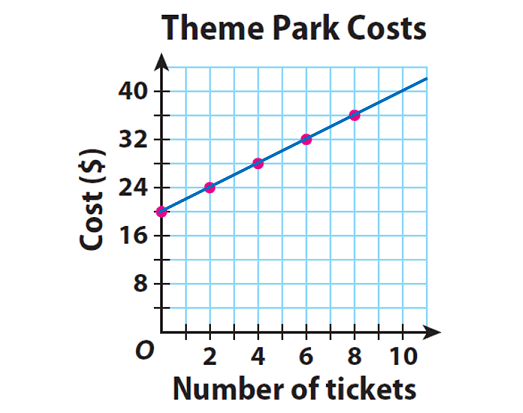
The points lie on a line.

Step 5 : 

Find the rate of change between each point and the next. Is the rate constant ?

Yes, the rate is constant. It is $2 per ticket.

Step 6 : 

Calculate y/x for the values in the table.

Explain why the relationship between number of tickets and total cost is not proportional. 

Undefined, 12, 7, about 5.3, 4.5 ;

The ratio of the total cost to the number of tickets sold is not constant, and the graph doesn’t pass through the origin.

Reflect

1.  Would it make sense to add more points to the graph from x = 0 to x = 10 ? 

Yes

We could add the points (1, 22), (3, 26), (5, 30), (7, 34), (9, 38), and (10, 40).

2.  Would it make sense to connect the points with a line ? Explain.

No

Because, the number of tickets can only be a whole number.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.