EVALUATING TRIGONOMETRIC FUNCTIONS FOR ANY ANGLE

Example 1 : 

Using the reference angle to evaluate sin 240°.

Solution : 

The angle 240° has its terminal side in quadrant III, as shown in figure below. 

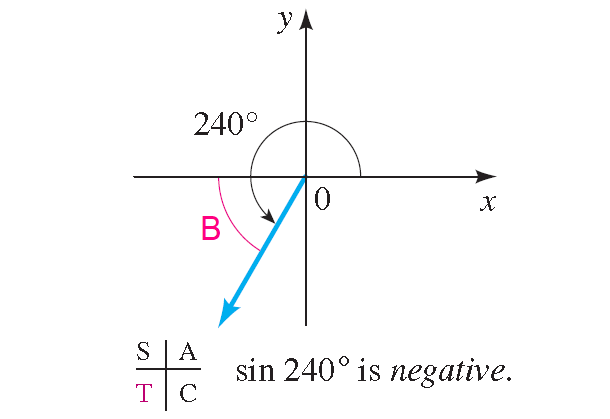
The reference angle is therefore

240° - 180°  =  60°,

and the value of sin 240° is negative. Thus

sin 240°  =  -sin 60°  =  √3/2

Example 2 : 

Using the reference angle to evaluate cot 495°.

Solution : 

The angle 495° is coterminal with the angle 135°, and the terminal side of this angle is in quadrant II, as shown in figure below. 

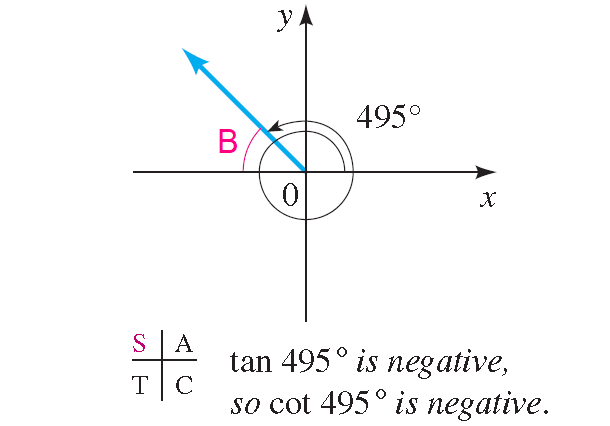
So the reference angle is

180° - 135°  =  45°,

and the value of cot 495° is negative. We have

cot 495°  =  cot 135°  =  -cot 45°  =  -1

Example 3 : 

Using the reference angle to evaluate sin 16π/3.

Solution : 

The angle 16π/3 is coterminal with 4π/3, and these angles are in quadrant III, as shown in the figure below. 

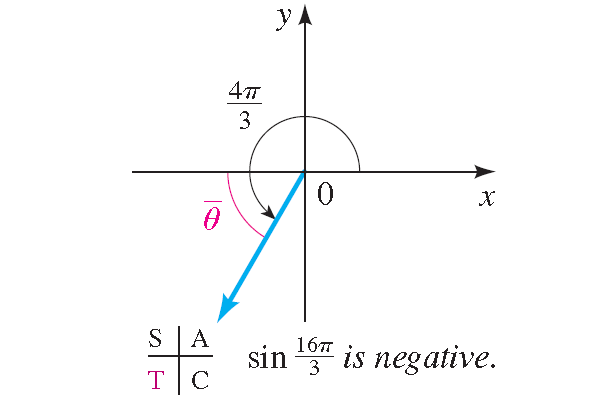
Thus, the reference angle is

4π/3 - π  =  π/3

Because the value of sine is negative in quadrant III, we have

sin 16π/3  =  sin 4π/3  =  -sin π/3  =  -√3/2

Example 4 : 

Using the reference angle to evaluate sec (-π/4).

Solution : 

The angle -π/4 is in quadrant IV, and its reference angle is π/4, as shown in the figure below. 

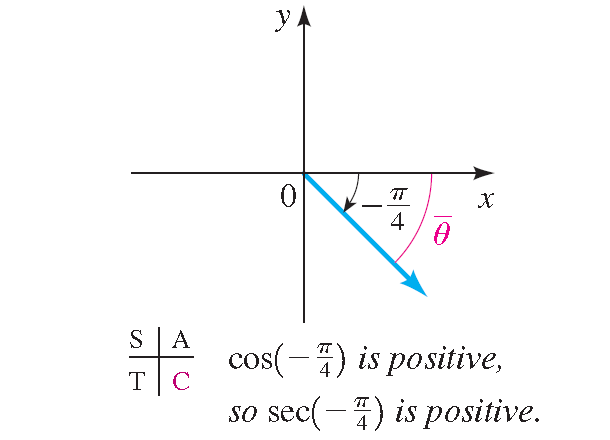
Because secant is positive in this quadrant, we get

sec (-π/4)  =  +sec (π/4)  =  √2/2

Example 5 :

Prove that

sin (8π/3) cos (23π/6) + cos (13π/3) sin (35π/6) = 1/2

Solution :

L.H.S :

sin (8π/3)

= (3π - 8π/3)

= (9π - 8π)/3

= π/3

Reference angle = π/3

sin (8π/3) = sin (π/3)

sin (8π/3) = √3/2

cos (23π/6)

= (4π - 23π/6)

= (24π - 23π)/6 

= π/6

cos (23π/6) = cos (π/6)

= √3/2

cos (13π/3)

= cos (4π + π/3)

= cos π/3

= 1/2

sin (35π/6)

= sin (6π - π/6)

= sin (6π - π/6)

Using ASTC, the angle 35π/6 lies in fourth quadrant. 

= -sin (π/6)

= -sin (π/6)

= - 1/2

sin (8π/3) cos (23π/6) + cos (13π/3) sin (35π/6)

= (√3/2)(√3/2) + (1/2)(-1/2)

= (3/4) - (1/4)

= (3 - 1) / 4

= 2/4

= 1/2

Example 6 :

tan (-225) cot (-405) - tan (-765) cot (675) = 0

Solution :

L.H.S :

tan (-225) cot (-405) - tan (-765) cot (675)

tan (-225) = - tan 225

225 lies in third quadrant,

reference angle = given angle - 180

= 225 - 180

= 45

Using ASTC, for the trigonometric ratios tan θ and cot θ, we will have positive sign. For other trigonometric ratios, we get negative sign.

-tan 225 = -tan 45

= -1

cot (-405) = - cot (405)

= -cot (360 + 45)

= -cot 45

It lies in the first quadrant,

= -1

tan (-765) = -tan (765)

= -tan (4 x 180 + 45)

= - tan 45

= -1

cot (675) = cot (4x180 - 45)

675 lies in fourth quadrant, for the trigonometric ratios cos θ and its reciprocal sec θ, we have positive sign. For other trigonometric ratios, we will get negative sign.

= -cot 45

= -1

tan (-225) cot (-405) - tan (-765) cot (675)

= -1(-1) - (-1) (-1)

= 1 - 1

= 0

Example 7 :

Prove that tan 720 - cos 270 - sin 150 cos 120 = 1/4

Solution :

L.H.S :

tan 720 - cos 270 - sin 150 cos 120

tan 720 = tan (4 x 180)

= tan 0

= 0

cos 270 = cos (180 + 90)

= cos 90

= 0

sin 150

Reference angle for 150

= 180 - 150

= 30

sin 150 = sin 30

= 1/2

cos 120

Reference angle for 120 = 180 - 120

= 60

cos 120 = -cos 60

= -1/2

tan 720 - cos 270 - sin 150 cos 120

= 0 - 0 - 1/2 (-1/2)

= 0 + 1/4

 = 1/4

Hence it is proved.

Example 8 :

sin 780 sin 480 + cos 120 sin 150 = 1/2

Solution :

L.H.S :

sin 780 sin 480 + cos 120 sin 150

sin 780 = sin (4 x 180 + 60)

= sin 60

Since angle 60 degree lies in the first quadrant, reference angle is also the same.

sin 60 = √3/2

sin 480 = sin (2 x 180 + 120)

= sin 120

120 lies in second quadrant, using ASTC for sin θ and its reciprocal cosec θ, we will have positive sign.

Reference angle for 120 degree is = 180 - given angle

= 180 - 120

= 60

= sin 60

= √3/2

cos 120 = cos (180 - 120)

= -cos 60

= - 1/2

sin 150 = sin (180 - 150)

= sin 30

= 1/2

sin 780 sin 480 + cos 120 sin 150

 =  (√3/2)  (√3/2) + (-1/2) (1/2)

= 3/4 - 1/4

= (3 - 1)/4

= 2/4

= 1/2

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.