EVALUATING NUMERIC EXPRESSIONS INVOLVING RATIONAL EXPONENTS

To evaluate numeric numeric values with rational exponents, we follow the steps given below.

Step 1 :

Express the base in exponential form.

Step 2 :

If we have power raised to another power, we will multiply the powers.

Step 3 :

Do possible simplification.

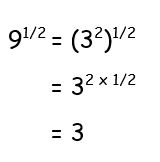
Evaluate the following :

Example 1 :

81^1/2

Solution :

= 81^1/2

Base = 81 and exponent = 1/2

81 = 9²

81^1/2 = (9²)^1/2

= 9^{(2 x 1/2)}

81^1/2 = 9

Example 2 :

16^3/2

Solution :

= 16^3/2

Base = 16, exponent = 3/2

16 = 4²

= 4^{(2 x 3/2)}

= 4³

16^3/2 = 64

Example 3 :

10000^3/4

Solution :

= 10000^3/4

Base = 10000 and exponent = 3/4

10000 = 10⁴

= 10^{(4 x 3/4)}

= 10³

= 1000

Example 4 :

64^2/3

Solution :

= 64^2/3

Base = 64 and exponent = 2/3

64 = 4³

= 4^{(3 x 2/3)}

= 4²

= 16

Example 5 :

27^2/3

Solution :

= 27^2/3

Base = 27 and exponent = 2/3

27 = 3³

= 3^{(3 x 2/3)}

= 3²

= 9

Example 6 :

81^-3/2

Solution :

= 81^-3/2

Base = 81 and exponent = -3/2

81 = 9²

= 9 ^{2 x (-3/2)}

= 9^-3

= 1/9³

= 1/729

Example 7 :

If c^2/5 = 4, then c = ?

Solution :

c^2/5 = 4

Raising power 5 on both sides.

(c^2/5)⁵ = 4⁵

c^{(2/5) x 5} = 4⁵

c² = 4⁵

Take square roots on both sides.

c = √4⁵

c = 4x4√4

c = 16√(2x2)

c = 16(2)

c = 32

Example 8 :

27^4/x = 81, x = ?

Solution :

27^4/x = 81

Try to express the bases 27 and 81 as a multiple of 3.

3³ = 27 and 3⁴ = 81

3^3(4/x) = 3⁴

3^12/x = 3⁴

Since the bases are equal, we can equate the powers.

12/x = 4

Take reciprocal on both sides.

x/12 = 1/4

Multiply 12 on both sides.

x = 12/4

x = 3

Example 9 :

20^1/2 ⋅ 20^1/2

Solution :

20^1/2 ⋅ 20^1/2

Using the property a^m ⋅ aⁿ = a^m+n

= 20^1/2 ⋅ 20^1/2

= 20^{(1/2 + 1/2)}

= 20

Example 10 :

5^1/3 ⋅ 25^1/3

Solution :

= 5^1/3 ⋅ 25^1/3

25 = 5²

= 5^1/3 ⋅ (5²)^1/3

= 5^1/3 ⋅ 5^2/3

= 5^(1+2)/3

= 5^3/3

= 5

Example 11 :

Evaluate 3 x (16)^3/4

Solution :

= 3 x (16)^3/4

16 = 2⁴

= 3 x (2⁴)^3/4

= 3 x 2^4x(3/4)

= 3 x 2³

= 3 x 8

= 24

So, 24 is the answer.

Example 12 :

Evaluate 2 x (27)^-2/3

Solution :

= 2 x (27)^-2/3

27 = 3³

= 2 x (3³)^-2/3

= 2 x 3^{3 x (-2/3)}

= 2 x 3^-2

= 2 x (1/3²)

= 2 x (1/9)

= 2/9

So, the answer is 2/9.

Example 13 :

Simplify

[(64)^-1/6x(216)^-1/3x(81)^1/4]/[(512)^-1/3x(16)^1/4x(9)^-1/2] 

Solution :

= [(64)^-1/6x(216)^-1/3x(81)^1/4]/[(512)^-1/3x(16)^1/4x(9)^-1/2]

Writting numbers in exponential form,

64 = 2⁶

216 = 6³

81 = 3⁴

512 = 8³

16 = 2⁴

9 = 3²

=[(64)^-1/6x(216)^-1/3x(81)^1/4]/[(512)^-1/3x(16)^1/4x(9)^-1/2] 

= (1/2) (1/6) 3 / (1/8) 2 (1/3)

= (3/12) / (2/24)

= (1/4) / (1/12)

= (1/4) x (12/1)

= 3

So, the answer is 3.

Example 14 :

Evalaute (0.000064)^5/6 

Solution :

= (0.000064)^5/6 

First we have to convert decimal as fraction, for that we observe the number of digits after the decimal. Since we have 6 digits after the decimal, we have to multiply the numerator and denominator by 1000000.

= [0.000064 x (1000000/1000000)]^5/6 

= [(64/1000000)]^5/6 

64 = 2⁶

= [2⁶/10⁶]^5/6 

= [(2/10)⁶]^5/6 

= (2/10)⁵

= 32/100000

= 0.00032

Example 15 :

Value of (27^1/3 + 64^1/3)² is

a)  7^1/3      b)  49     c)  7^1/2      d)  1/7

Solution :

= (27^1/3 + 64^1/3)² 

Writing 27 and 64 in exponential form, we get

(27^1/3 + 64^1/3)² = (3 + 4)²

= 7²

= 49

So, option b is correct.

Example 16 :

Value of ((625)^-1/2)² is

a)  1/625      b)  -25     c)  -625      d)  25

Solution :

= ((625)^-1/2)²

625 = 25 x 25

= 25²

((625)^-1/2)² = ((25²)^-1/2)²

= 25^-2

= 1/25²

= 1/625

So, option a is correct.

Solve the given exponential equations.

Example 17 :

Value of (√6)^{x - 2} = 1

Solution :

(√6)^{x - 2} = 1

Anything to the power 0 is 1.

(√6)^{x - 2} = 6⁰

Writing square root sign in exponential form, we get

(6)^{(x - 2)/2} = 6⁰

Since the bases are equal, we can equate the powers.

(x - 2)/2 = 0

x - 2 = 0

x = 2

So, the value of x is 2.

Example 18 :

Value of 4 x (81)^-1/2 [81^1/2 + 81^3/2]

Solution :

= 4 x (81)^-1/2 [81^1/2 + 81^3/2]

81 = 9²

= 4 x (9²)^-1/2 [(9²)^1/2 + (9²)^3/2]

= 4 x (9^-1) [9^2x(1/2) + 9^{2 x (3/2)}]

= 4 x (1/9) [9 + 9³]

= (4/9) [9 + 729]

= (4/9)(738)

= 4(82)

= 328

Example 19 :

Value of (64)^1/2 [64^1/2 + 1]

Solution :

= (64)^1/2 [64^1/2 + 1]

64 = 8²

= (8²)^1/2 [(8²)^1/2 + 1]

= 8^{2 x (1/2)} [8^{2 x (1/2)} + 1]

= 8 [8 + 1]

= 8 (9)

= 72

Example 20 :

Value of [(36)^7/2 - (36)^9/2] / (36)^5/2

Solution :

= [(36)^7/2 - (36)^9/2] / (36)^5/2

36 = 6²

= [(6²)^7/2 - (6²)^9/2] / (6²)^5/2

= [6⁷ - 6⁹] / 6⁵

= [6⁵ (6² - 6⁴)] / 6⁵

= (6² - 6⁴)

= 36 - 1296

= 1260

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.