EVALUATING ALGEBRAIC EXPRESSIONS

Example 1 :

Evaluate the expression for the given value of the variable.

x - 9; x = 15

Solution :

15 - 9 = 6

Therefore, when x = 15, x - 9 = 6.

Example 2 :

Evaluate the expression for the given value of the variable.

16/n; n = 8

Solution :

16/8 = 2

Therefore, when n  =  8, 16/n = 2.

Example 3 :

Evaluate the given expression for x = 3 and y = 5. 

3x + 2y

Solution :

Substitute x = 3 and y = 5 in the given expression

= 3(3) + 2(5)

 = 9 + 10

= 19

Therefore, 3x + 2y = 19.

Example 4 :

Evaluate the given expression for y = 1.4. 

0.5y

Solution :

Substitute y = 1.4 in the given expression

= 0.5(1.4)  

= 0.5 x 1.4 

= 0.7

Therefore, 0.5y = 0.7.

Example 5 :

Evaluate the given expression for s = 5. 

s² + 7s - 2

Solution :

Substitute s = 5 in the given expression

= 5² + 7(5) - 2  

= 25 + 35 - 2  

= 58

Therefore, s² + 7s - 2 = 58.

Example 6 :

Evaluate the given expression for m = 1/3. 

18m² + 3m + 7

Solution :

Substitute m = 1/3 in the given expression

= 18(1/3)² + 3(1/3) + 7  

= 2 + 1 + 7  

= 10

Therefore, 18m² + 3m + 7 = 10.

Example 7 :

Evaluate the given expression for m = 13. 

m² + m - 54

Solution :

Substitute m = 13 in the given expression.

= 13² + 13 -54  

= 169 + 13 - 54  

= 128

Therefore, m² + m - 54 = 128.

Example 8 :

Evaluate the given expression for x = 3 and y = 5. 

x² + y²

Solution :

Substitute x = 3 and y = 5 in the given expression.

= 3² + 5²  

= 9 + 25  

= 34

Therefore, x² + y² = 34.

Example 9 :

Evaluate the given expression for m = 5  and n = 2. 

5m² + 2m²n

Solution :

Substitute m = 5 and n = 2 in the given expression.

= 5(5)² + 2(5)²(2)  

= 125 + 100 

= 225

Therefore, 5m² + 2m²n = 225.

Example 10 :

Evaluate the given expression for m = 3. 

(2m² + 5m - 7)/2

Solution :

Substitute m = 3 in the given expression

= [2(3)² + 5(3) - 7]/2

 = [18 + 15 - 7]/2

= 26/2

 = 13

Therefore, (2m² + 5m - 7)/2 = 13.

Example 11 :

You buy foam spheres, paint bottles, and wooden rods to construct a model of our solar system. What is your total cost?

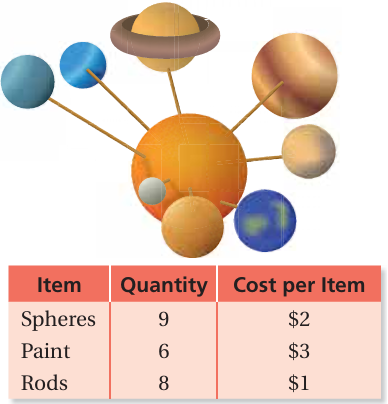
Solution :

Number of spheres = 9

Number of paint = 6

Number of rods = 8

Total cost = 9(2) + 6(3) + 8(1)

= 18 + 18 + 8

= 44

So, the total cost is $44.

Example 12 :

You have four $10 bills and eighteen $5 bills in your piggy bank. How much money do you have?

Solution :

Number of $10 bill = 4

Number of$5 bill = 18

Total amount in the piggy bank = 4(10) + 5(18)

= 40 + 90

= 130

So, the total amount i have in my piggy bank is $130.

Example 13 :

Before a show, there are 8 people in a theater. Five groups of 4 people enter, and then three groups of 2 people leave. Evaluate the expression 8 + 5(4) − 3(2) to fi nd how many people are in the theater

Solution :

= 8 + 5(4) − 3(2)

= 8 + 20 - 6

= 28 - 6

= 22

So, there are 22 people.

Example 14 :

An auditorium has a total of 592 seats. There are 37 rows of seats, and each row has the same number of seats. How many seats are there in a single row?

Solution :

Total number of seats = 592

Total number of rows = 37

Each row consist of same number of seats.

Total number of seats in each row = 592/37

= 16

So, there are 16 seats in each row.

Example 15 :

Erica was evaluating the expression in the box below.

56 ÷ (23 − 1) × 4 = 56 ÷ (8 − 1) × 4

= 56 ÷ 7 × 4

= 56 ÷ 28

= 2

What should Erica do to correct the error that she made? 

a) Divide 56 by 8 because operations are performed left to right.

b) Multiply 1 by 4 because multiplication is done before subtraction.

c) Divide 56 by 7 because operations are performed left to right.

d) Divide 56 by 8 and multiply 1 by 4 because division and multiplication are performed before subtraction.

Solution :

c) Divide 56 by 7 because operations are performed left to right.

= 56 ÷ (8 − 1) × 4

= 56 ÷ 7 × 4

= 8 x 4

= 32

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.