EVALUATE THE INDICATED VALUE OF COMPOSITION FUNCTION FROM THE TABLE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Problem 1 :
Evaluate the indicated expression assuming that f, g, and h are the functions completely defined by the tables below :
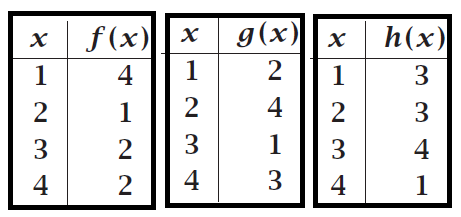
(i) (f o g) (1)
(ii) (f o g) (3)
(iii) (g o f) (1)
(iv) (g o f) (3)
(v) (f o f) (2)
(vi) (f o g o h) (2)
(vii) (h o g o f) (2)
Solution :
(i) (f o g) (1)
(f o g) (1) = f[g(1)]
= f(2)
= 1
(ii) (f o g) (3)
(f o g) (3) = f[g(3)]
= f(1)
= 4
(iii) (g o f) (1)
(g o f) (1) = g[f(1)]
= g(4)
= 3
(iv) (g o f) (3)
(g o f) (3) = g[f(3)]
= g(2)
= 1
(v) (f o f) (2)
(f o f) (2) = f[f(2)]
= f(1)
= 4
(vi) (f o g o h) (2)
(f o g o h) (2) = (f o g)[h(2)]
= (f o g) (3)
= f[g(3)]
= f(1)
= 4
(vii) (h o g o f) (2)
(h o g o f) (2) = (h o g)[f(2)]
= (h o g) (1)
= h[g(1)]
= h(2)
= 3
Problem 2 :
Use the values in the table to evaluate the indicated composition of functions.
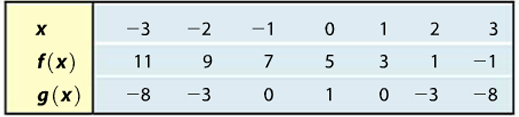
a) (f o g) (1)
b) (f o g) (2)
c) (g o f) (2)
d) (g o f) (3)
e) (g o g) (1)
f) (f o f) (3)
Solution :
a) (f o g) (1) = f[g(1)]
From the table, the value of g(1) is 0.
= f(0)
The value of f(0) is 5
= 5
So, the value of (f o g) (1) is 5.
b) (f o g) (2) = f[g(2)]
The value of g(2) is -3. Applying that
= f(-3)
The value of f(-3) is 11
= 11
So, the value of (f o g) (2) is 11.
c) (g o f) (2) = g[f(2)]
The value of f(2) is 1. Applying that,
= g(1)
The value of g(1) is 0
So, the value of (g o f) (2) is 0.
d) (g o f) (3) = g[f(3)]
The value of f(3) is -1. applying that
= g(-1)
The value of g(-1) is 0.
So, the value of (g o f) (3) is 0.
e) (g o g) (1) = g[g(1)]
The value of g(1) is 0. applying that
= g(0)
The value of g(0) is 1.
So, the value of (g o g) (1) is 1.
f) (f o f) (3) = f[f(3)]
The value of f(3) is -1.
= f[-1]
The value of f(-1) is 7.
So, the value (f o f) is 7.
The accompanying tables define functions f and g.
Problem 3 :
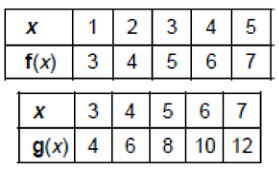
What is (g o f)(3) ?
a) 6 b) 2 c) 8 d) 4
Solution :
(g o f)(3) = g[f(3)]
From the table, the value of f(3) is 5.
= g(5)
The value of g(5) is 8.
So, the value of (g o f)(3) is 8. So, option c is correct.
Problem 4 :
Use the table of values to evaluate each expression
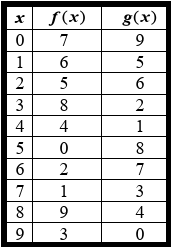
|
a) f(g(8)) b) f(g(5)) c) g(f(5)) d) g(f(3)) |
e) f(f(4)) f) f(f(1)) g) g(g(2)) h) g(g(6)) |
Solution :
a) f(g(8))
The value of g(8) from the table, we get g(8) = 4
= f(4)
The value of f(4) is 4.
So, the value of f(g(8)) is 4.
b) f(g(5))
From the table, the value of g(5) is 8.
= f(8)
The value of f(8) is 9.
So, the value of f(g(5)) is 9.
c) g(f(5))
From the table, the value of f(5) is 0.
= g(0)
The value of g(0) is 9.
So, the value of g(f(5)) is 9.
d) g(f(3))
From the table, the value of f(3) is 8.
= g (8)
The value of g(8) is 4.
So, the value of g(f(3)) is 4.
e) f(f(4))
The value of f(4) is 4
= f(4)
The value f(4) is 4.
So, the value of f(f(4)) is 4.
f) f(f(1))
The value of f(1) is 6.
= f(6)
The value of f(6) is 2.
So, the value of f(f(1)) is 2.
g) g(g(2))
The value of g(2) is 6.
= g(6)
The value of g(6) is 7.
So, the value of g(g(2)) is 7.
h) g(g(6))
The value of g(6) is 7.
= g(7)
The value of g(7) is 3.
So the value of g(g(6)) is 3.
Problem 5 :
Functions f and g consist only of the ordered pairs shown. Find the ordered pairs for y = f(g(x)).
f: (−12, 11), (−4, 9), (1, 3), (2, −4), (6, −5)
g: (−10, 6), (−3, 1), (0, −4), (5, 2), (8, −12)
Solution :
y = f(g(x))
Inputs are from the function g.
|
When x = -10 y = f(g(-10)) y = f(6) y = -5 |
When x = -3 y = f(g(-3)) y = f(1) y = 3 |
|
When x = 0 y = f(g(0)) y = f(-4) y = 9 |
When x = 5 y = f(g(5)) y = f(2) y = -4 |
When x = 8
y = f(g(8))
y = f(-12)
y = 11
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 43)
Jan 04, 26 01:38 AM
10 Hard SAT Math Questions (Part - 43) -
90 Degree Clockwise Rotation
Jan 01, 26 06:58 AM
90 Degree Clockwise Rotation - Rule - Examples with step by step explanation -
US Common Core K-12 Curriculum Algebra Solving Systems of Equations
Jan 01, 26 04:51 AM
US Common Core K-12 Curriculum - Algebra : Solving Systems of Linear Equations
