EVALUATE THE FUNCTION FOR THE GIVEN VALUES OF X

About "Evaluate the Function for the Given Values of x"

Evaluate the Function for the Given Values of x :

Here we are going to see some example problems to understand evaluating the functions for the given values of x.

Evaluate the Function for the Given Values of x - Questions

Question 1 :

Given the function f : x -> x² −5x + 6 , evaluate

(i) f (-1)

(ii) f (2a)

(iii) f (2)

(iv) f (x −1)

Solution :

Given that :

f(x)  =  x² −5x + 6

(i) f (-1)

here we have -1 instead of x.

f(-1)  =  (-1)² −5(-1) + 6

  =  1 + 5 + 6

f(-1)  =  12

(ii) f (2a)

here we have 2a instead of x.

f(2a)  =  (2a)² −5(2a) + 6

  =  4a² - 10a + 6

(iii) f (2)

here we have 2 instead of x.

f(2)  =  (2)² −5(2) + 6

  =  4 - 10 + 6

=  0

(iv) f (x −1)

here we have x - 1 instead of x.

f(x-1)  =  (x-1)² −5(x-1) + 6

  =  x² - 2x + 1 - 5x + 5 + 6

=  x² - 7x + 12

Question 2 :

A graph representing the function f (x) is given figure

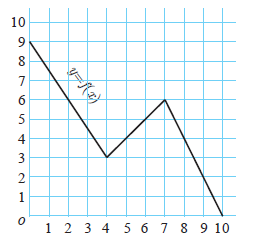
it is clear that f (9) = 2.

(i) Find the following values of the function

(a) f (0) (b) f (7) (c) f (2) (d) f (10)

(ii) For what value of x is f (x) = 1?

(iii) Describe the following (i) Domain (ii) Range.

(iv) What is the image of 6 under f ?

Solution :

(i)  

(a)  f(0)  =  9,  (b)  f(7)  =  6,  (c) f (2)  =  6,  (d) f (10)  =  0

(ii) For what value of x is f (x) = 1 ?

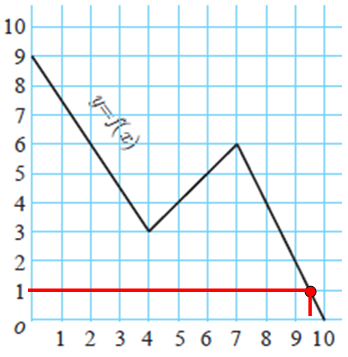
For x = 9.5, we get 1.

(iii) Describe the following (i) Domain (ii) Range.

Domain  =  { 0 ≤ x  ≤ 10 }

Range  =  { 0 ≤ x  ≤ 9 }

(iv) What is the image of 6 under f ?

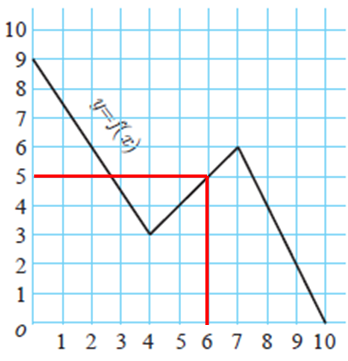
Question 3 :

Let f (x) = 2x + 5. If x ≠ 0 then find [f(x + 2) - f(2)] / x

Solution :

f (x) = 2x + 5

f(x + 2)  =  2(x + 2) + 5

f(x + 2)  =  2x + 4 + 5   -------(1)

f(x + 2)  =  2x + 9

f(2)  =  2(2) + 5 

  =  4 + 5

f(2)  =  9  -------(2)

(1) - (2)   =  2x + 9 - 9

  =  2x

[f(x + 2)  - f(2) ]/x  =  2x / x  =  2

Question 4 :

A function f is defined by f (x) = 2x – 3

(i) find [f(0) +  f(1)]/2

(ii) find x such that f (x) = 0.

(iii) find x such that f (x) = x .

(iv) find x such that f (x) = f (1−x) .

Solution :

f(x) = 2x – 3

(i)  [f(0) +  f(1)]/2

f(0)  =  2(0) - 3  =  -3

f(1)  =  2(1) - 3  =  -1

[f(0) +  f(1)]/2  =  [-3 + (-1)] / 2

  =  -4/2

  =  -2

Hence the answer is -2.

(ii) find x such that f (x) = 0.

f(x) = 2x – 3

2x - 3  =  0

2x  =  3

x  =  3/2 

Hence the answer is 3/2.

(iii) find x such that f (x) = x .

f(x) = 2x – 3

2x - 3  =  x

2x - x  =  3

x  =  3

Hence the answer is 3

(iv) find x such that f (x) = f (1−x) .

f(1 - x)  =  2(1- x) - 3

  =  2 - 2x - 3

  =  -2x - 1

2x - 3  =  -2x - 1

2x + 2x  =  - 1 + 3

4x  =  2

x  =  2/4  =  1/2

Hence the answer is 1/2.

After having gone through the stuff given above, we hope that the students would have understood, "Evaluate the Function for the Given Values of x". 

Apart from the stuff given in this section "Evaluate the Function for the Given Values of x", if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.