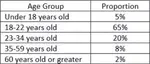
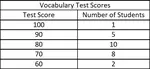
EVALUATE ABSOLUTE VALUE EXPRESSIONS

Example 1 :

Evaluate the following absolute value expression

|x + 6| - 4 for x = -3

Solution :

|x + 6| - 4 for x = -3

In order to evaluate the given absolute value expression, we have to apply the value -3 instead of the variable x.

  =  |-3 + 6| - 4 

  =  |3| - 4

  =  3 - 4 = -1

Hence, the answer is -1.

Example 2 :

Evaluate the following absolute value expression

|-8 - x| + 3 for x = -1

Solution :

|-8 - x| + 3 for x = -1

In order to evaluate the given absolute value expression, we have to apply the value -1 instead of the variable x.

  =  |-8 - (-1)| + 3

  =  |-8 + 1| + 3

  =  |-7| + 3

  =  7 + 3

=  10

Hence, the answer is 10.

Example 3 :

Evaluate the following absolute value expression

8 + |8 - x| + |x - 2| for x = 0

Solution :

8 + |8 - x| + |x - 2|

In order to evaluate the given absolute value expression, we have to apply the value 0 instead of the variable x.

  =  8 + |8 - 0| + |0 - 2|

  =  8 + |8| + |- 2|

  =  8 + 8 + 2

=  18

Hence, the answer is 18.

Example 4 :

Evaluate the following absolute value expression

7 + |3 - 2x| + |5x - 7| for x = -3

Solution :

7 + |3 - 2x| + |5x - 7|

In order to evaluate the given absolute value expression, we have to apply the value -3 instead of the variable x.

  =  7 + |3 - 2(-3)| + |5(-3) - 7|

  =  7 + |3 + 6| + |-15 - 7|

  =  7 + |9| + |-22|

  =  7 + 9 + 22

=  38

Hence, the answer is 38.

Example 5 :

Evaluate the following absolute value expression

-x + |7 - 4x| + |2x - 1| for x = -2

Solution :

-x + |7 - 4x| + |2x - 1|

In order to evaluate the given absolute value expression, we have to apply the value -2 instead of the variable x.

  =  -(-2) + |7 - 4(-2)| + |2(-2) - 1|

  =  2 + |7 + 8| + |-4 - 1|

  =  2 + |15| + |-5|

  =  2 + 15 + 5

=  22

Hence, the answer is 22.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.