ESTIMATING LIMITS FROM TABLES

Here we are going to see how to find a limit using a table.

Before look into example problems, first let us see the meaning of the word "Limit"

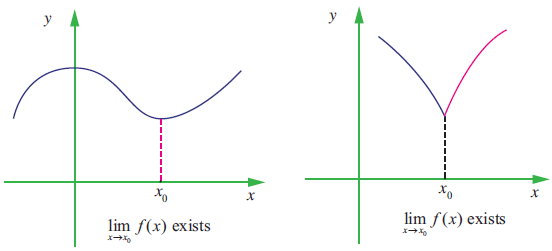
Let I be an open interval containing x₀∈ R. Let f : I -> R. Then we say that the limit of f(x) is L, as x approaches x₀ [Usually written as lim _{x -> 0}f(x) = L], if, whenever x becomes sufficiently close to x₀ from either side with x ≠ x₀gets sufficiently close to L.

Question 1 :

Complete the table using calculator and use the result to estimate the limit.

lim _x->-3 (√(1-x) - 2)/(x + 3)

Solution :

if x = -3.1

f(x) = lim _x->-3 (√(1-x) - 2)/(x + 3)

f(-3.1) = (√(1+3.1) - 2)/(-3.1 + 3)

= (√4.1 - 2)/(-0.1)

= -0.24846

if x = -3.01

f(-3.01) = (√(1+3.01) - 2)/(-3.01 + 3)

= (√4.01 - 2)/(-0.01)

= -0.2498

if x = -3.0

f(3.0) = (√(1+3) - 2)/(-3 + 3)

= (√4 - 2)/0

= Indeterminant form

if x = -2.999

f(-2.999)=(√(1+2.999)-2)/(-2.999+3)

= -0.25001

if x = -2.99

f(-2.99)=(√(1+2.99)-2)/(-2.99+3)

= - 0.2501

if x = -2.9

f(-2.9)=(√(1+2.9)-2)/(-2.9+3)

= -0.2515

From the above table, we have to estimate the limit when x tends to -3.

When x approaches - 3, f(x) tends to -0.25 approximately.

Hence the answer is -0.25

Question 2 :

lim _x->0 sin x/x

Solution :

if x = -0.1

f(x) = lim _x->0 sin x/x

f(-0.1) = sin (-0.1)/(-0.1)

= -sin (0.1)/(-0.1)

= 0.99833

if x = -0.01

f(x) = lim _x->0 sin x/x

f(-0.01) = sin (-0.01)/(-0.01)

= -sin (0.01)/(-0.01)

= 0.9998

if x = -0.001

f(x) = lim _x->0 sin x/x

f(-0.001) = sin (-0.001)/(-0.001)

= -sin (0.001)/(-0.001)

= 0.9999

if x = 0.001

f(x) = lim _x->0 sin x/x

f(0.001) = sin (0.001)/(0.001)

= sin (0.001)/0.001

= 0.9999

if x = 0.01

f(x) = lim _x->0 sin x/x

f(0.01) = sin (0.01)/(0.01)

= 0.99998

if x = 0.1

f(x) = lim _x->0 sin x/x

f(0.1) = sin (0.1)/(0.1)

= 0.99833

Here x->0 appears between -0.001 to 0.001. By observing the table, we may estimate the limit as 0.99

Hence the answer is 0.99

Question 3 :

lim _{x -> 0}(cos x - 1)/x