ESTIMATING LIMIT VALUES FROM GRAPHS

Condition Required for Existence of Limit of a Function

lim x->x₀ f(x)  =  L exists if the following hold :

(i) lim x->x₀+ f(x) exists, 

(ii)  lim x->x₀- f(x) exists, and

(iii)  lim x->x₀+ f(x)  =   lim x->x₀- f(x)  =  L

Solved Problems

Problem 1 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->1  sin πx

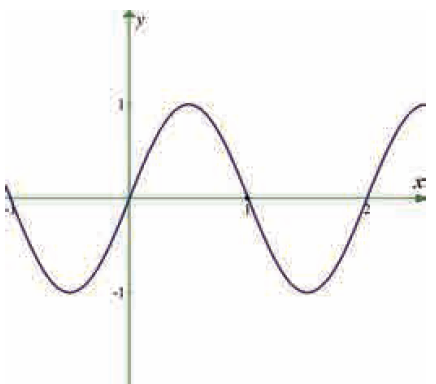
Solution :

When 1 approaches from left hand side, we get the value closer to 0.

When 1 approaches from right hand side, we get the value closer to 0.

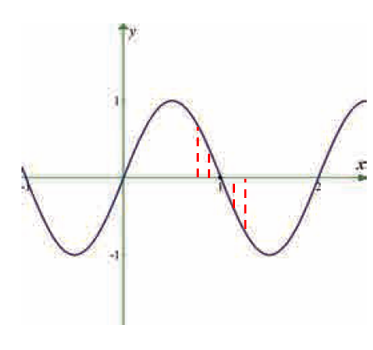
Hence the required limit 0.

Problem 2 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->1  sec x

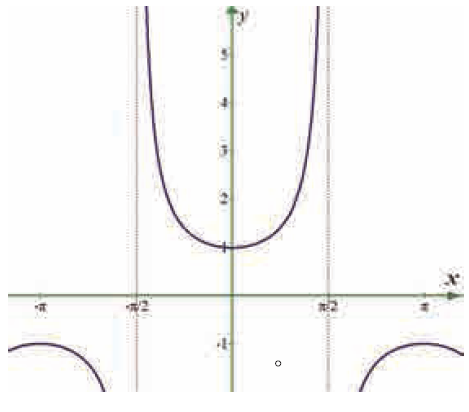
Solution :

When 1 approaches from left hand side, we get the value closer to 1.

When 1 approaches from right hand side, we get the value closer to 1.

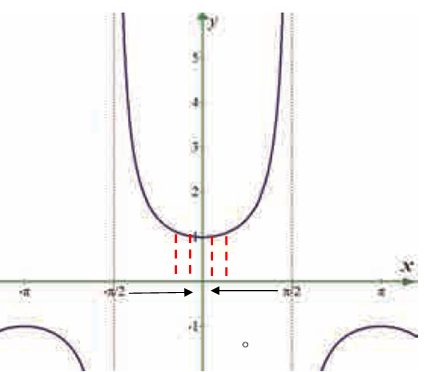
Hence the required limit 1.

Problem 3 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->π/2 tan x 

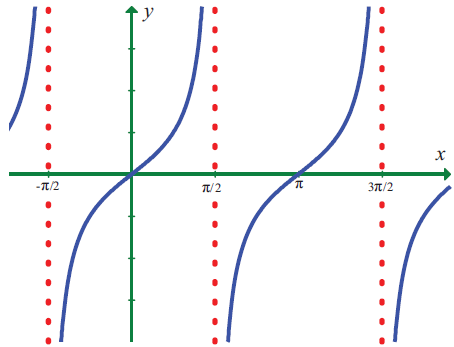
Solution :

When 1 approaches from left hand side, we get the value closer to 1.

When 1 approaches from right hand side, we get the value closer to 1.

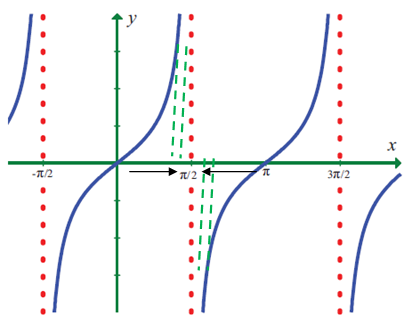
Hence the function does not exist.

Problem 4 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->1 f(x) 

Where f(x)  =  x² + 2      x ≠ 1

                    =    1            x = 1

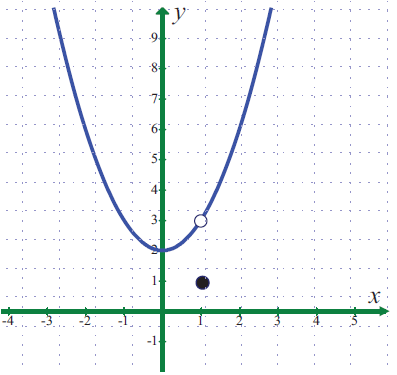
Solution :

To find the value of left hand limit and right hand limit for x -> 1, we have to use the function f(x)  =  (x² + 2). It is enough to check if we get equal values for left hand and right hand limit.

lim _x->1^- f(x)  =  lim _x->1+ f(x)

Hence the required limit is 3.

Problem 5 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->3 1/(x- 3)

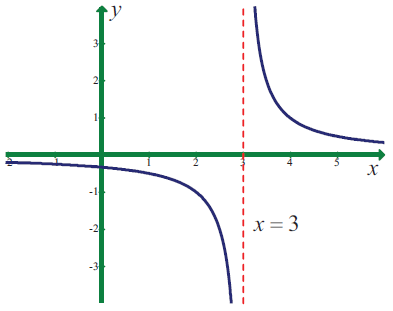
Solution :

From the graph given above, we get different values for left hand limit and right hand limit.

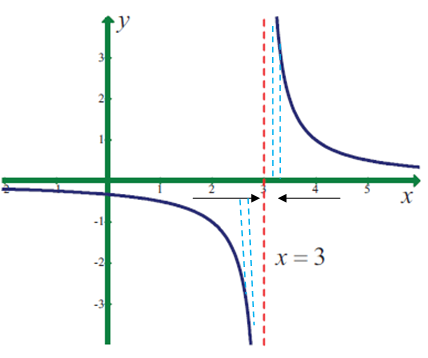
The function does not exist at x - >3.

Problem 6 :

Use the graph to find the limits (if it exists). If the limit does not exist, explain why?

lim _x->5 |x - 5|/(x - 5)

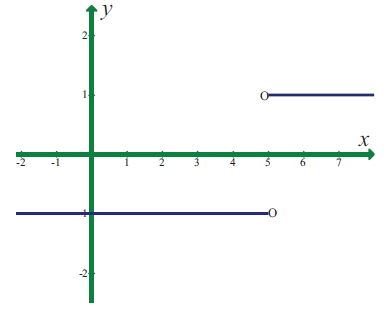
Solution :

From the graph given above, we get different values for left hand limit and right hand limit.

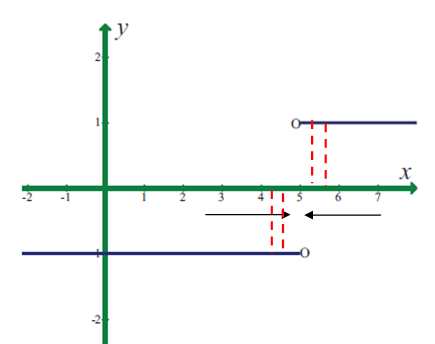
The function does not exist at x - >5.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.