ESTIMATING IRRATIONAL NUMBERS WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Question 1 :
Estimate the value of the irrational number √2.
Question 2 :
Draw a number line and locate your estimation of √2.
Question 3 :
How could you find an even better estimate of √2 ?
Question 4 :
Find a better estimate of √2 . Draw a number line and locate and label your estimate.
Question 5 :
Find a better estimate of √7 . Draw a number line and locate and label your estimate.

Answers
Question 1 :
Estimate the value of the irrational number √2.
Answer :
A. Since 2 is not a perfect square, √2 is irrational.
B. To estimate √2 , first find two consecutive perfect squares that 2 is between. We can do this by writing the following inequality.
1 < 2 < 4
C. Now take the square root of each number.
D. Simplify the square roots of perfect squares.
√2 is between 1 and 2
E. Estimate that √2 ≈ 1.5.
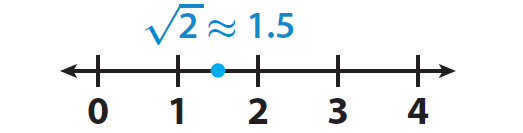
F. To find a better estimate, first choose some numbers between 1 and 2 and square them.
For example, choose 1.3, 1.4, and 1.5.
1.32 = 1.69, 1.42 = 1.96, 1.52 = 2.25
Is √2 between 1.3 and 1.4 ? How do we know ?
No ; √2 is not between 1.69 and 1.96.
Is √2 between 1.4 and 1.5 ? How do we know ?
Yes ; √2 is between 1.96 and 2.25.
Since √2 is between 1.4 and 1.5, we have √2 ≈ 1.45.
Question 2 :
Draw a number line and locate your estimation of √2.
Answer :
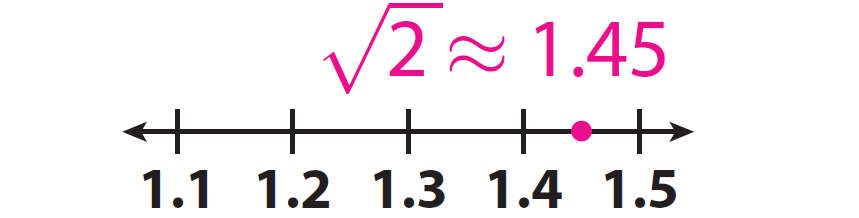
Question 3 :
How could you find an even better estimate of √2 ?
Answer :
Test the squares of numbers between 1.4 and 1.5.
Question 4 :
Find a better estimate of √2 . Draw a number line and locate and label your estimate.
Answer :
√2 is between 1.41 and 1.42. So, √2 ≈ 1.415.
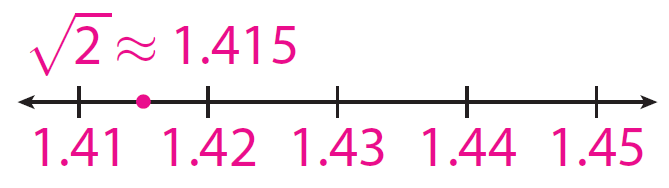
Question 5 :
Find a better estimate of √7 . Draw a number line and locate and label your estimate.
Answer :
√7 is between 2.6 and 2.7. So, √7 ≈ 2.65.
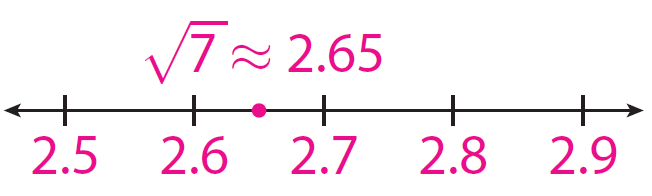
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

