EQUIVALENT RATIOS WORKSHEET

1. Write three ratios which are equivalent to the ratio given below.

2/3

2. Write four ratios which are equivalent to the ratio given below.

5/4

3. Write three ratios which are equivalent to 5⅓.

4. Write three ratios which are equivalent to 0.8.

5. David makes 5 cups of punch by mixing 3 cups of cranberry juice with 2 cups of apple juice. How much cranberry juice and how much apple juice does David  need to make four times the original recipe ?

6. Alex makes an alloy by mixing two types of metals, say A and B. To make one unit of alloy, he needs 12 grams of metal A and 17 grams of metal B. If he makes, 5 units  of alloy, how many grams of metal A and metal B does he need ?

1 Answer :

(2/3) x (2/2) = 4/6

(2/3) x (3/3) = 6/9

(2/3) x (4/4) = 8/12

Three ratios which are equivalent to the ratio 2/3 are

4/6, 6/9 and 8/12

2. Answer :

(5/4) x (2/2) = 10/8

(5/4) x (3/3) = 15/12

(5/4) x (4/4) = 20/16

(5/4) x (5/5) = 25/20

Four ratios which are equivalent to the ratio 8/10 are

10/8, 15/12, 20/16 and 25/20

3. Answer :

5⅓

Convert the given mixed number to an improper fraction.

5⅓ = 16/3

(16/3) x (2/2) = 32/6

(16/3) x (3/3) = 48/9

(16/3) x (4/4) = 64/12

Three ratios which are equivalent to 5⅓ are

32/6, 48/9 and 64/12

4. Answer :

0.8

Convert the decimal number 0.8 to a fraction.

0.8 = 8/10 = 4/5

(4/5) x (2/2) = 8/10

(4/5) x (3/3) = 12/15

(4/5) x (4/4) = 16/20

Three ratios which are equivalent to the ratio 0.8 are

4/5, 12/15 and 16/20

5. Answer :

Make a table comparing the numbers of cups of cranberry juice and apple juice needed to make two times, three times, four times, and five times the original recipe.

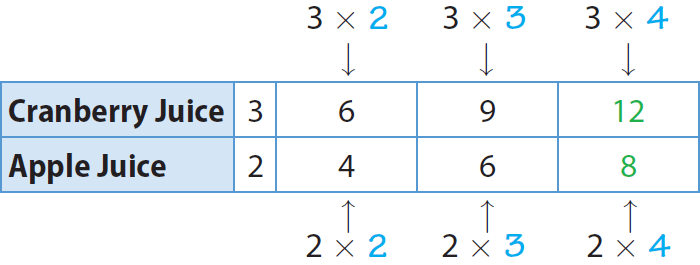
In the above table, both terms of the original ratio are multiplied by the same number to find an equivalent ratio.

The last column of the table shows the numbers of cups of the two juices David needs for four times the original recipe.

David needs 12 cups of cranberry juice and 8 cups of apple juice.

6. Answer :

Alex needs 12 grams of metal A and 17 grams of metal B to make 1 unit of alloy.

From the above information, the ratio between metal A and metal B to make 1 unit of alloy is

12/17

Since Alex makes 5 units of alloy, we have to multiply the numerator and denominator of the above ratio by 5.

(12/17) x (5/5) = 60/85

To make 5 units of alloy, Alex needs 60 grams of metal A and 85 grams of metal B.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.