EQUATIONS OF CIRCLES WORKSHEET

Problem 1 :

Write the standard equation of the circle whose center is (-4, 0) and radius is 7.

Problem 2 : 

Write the standard equation of the circle whose general equation is

x² + y² - 4x + 6y - 12  =  0

Problem 3 : 

The point (1 ,2) is on a circle whose center is (5, -1).  Write the standard equation of the circle.

Problem 4 :

The equation of a circle is 

(x + 2)² + (y - 3)²  =  9

Graph the circle.

Problem 5 :

A bank of lights is arranged over a stage. Each light illuminates a circular area on the stage. A coordinate plane is used to arrange the lights, using the corner of stage as the origin. The equation  (x - 13)² + (y - 4)²  =  16 represents one of the disks of light. 

(i)  Graph the disk of light. 

(ii)  Three actors are located as follows : 

Henry is at (11, 4)

Jolene is at (8, 5)

Martin is at (15, 5)

Which actors are in the disk of light ? 

Answers

1. Answer :

Given : Center = (-4, 0) and radius = 7.

Standard equation of a circle. 

(x - h)² + (y - k)²  =  r²

Substitute (h, k) = (-4, 0) and r = 7.

[x - (-4)²] + (y - 0)²  =  7²

Simplify. 

(x + 4)² + y²  =  49

2. Answer :

x² + y² - 4x + 6y - 12  =  0

To find the standard equation of the circle, we need to know the center and radius. 

Let us find the center and radius from the given general equation of the circle. 

Comparing 

x² + y² + 2gx + 2fy + c  =  0

and

x² + y² - 4x + 6y - 12  =  0,

we have 

2g  =  - 4 -----> g  =  -2

2f  =  6 -----> f  =  3

c  =  -12

Center  =  (-g, -f)  =  (2, -3)

Radius  =  √[g² + f² - c]

Radius  =  √[(-2)² + 3² - (-12)]

Radius  =  √[4 + 9 + 12]

Radius  =  √25

Radius  =  5

Standard equation of a circle : 

(x - h)² + (y - k)²  =  r²

Substitute (h, k)  =  (2, -3) and r  =  5.

(x - 2)² + [y - (-3)²]  =  5²

Simplify. 

(x - 2)² + (y + 3)²  =  25

3. Answer :

Given : The point (1, 2) is on the circle and center of the circle is (5, -1).

To find the standard equation of the circle, we need to know the center and radius. The center is already given and we need to find the radius.

Using distance formula, we have

Radius  =  √[(5 - 1)² + (-1 - 2)²]

Radius  =  √[4² + (-3)²]

Radius  =  √[16 + 9]

Radius  =  √25

Radius  =  5

Standard equation of a circle : 

(x - h)² + (y - k)²  =  r²

Plug (h, k)  =  (5, -1) and r  =  5.

(x - 5)² + [y - (-1)²]  =  5²

Simplify. 

(x - 5)² + (y + 1)²  =  5²

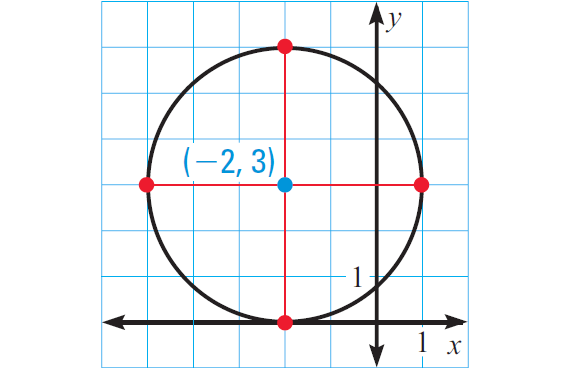
4. Answer :

(x + 2)² + (y - 3)²  =  9

To graph a circle, we need to know the radius and center of the circle.

Rewrite the equation to find the center and radius. 

(x + 2)² + (y - 3)²  =  9

[x - (-2)²] + (y - 3)²  =  3²

So, the center is (-2, 3) and the radius is 3. 

To graph the circle, place the point of a compass at (-2, 3), set the radius at 3 units and swing the compass to draw a full circle. 

5. Answer :

Solution (i) : 

To graph the disk of light, we need to know the center and radius of the circle.

Rewrite the equation to find the center and radius. 

(x - 13)² + (y - 4)²  =  16

(x - 13)² + (y - 4)²  =  4²

So, the center is (13, 4) and the radius is 4. 

The circle with center at (13, 4) and radius 4 units shown below (Graph of the disk of light).

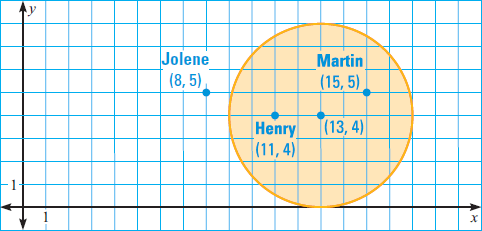
Solution (ii) : 

The graph given above shows that Henry and Martin are both in the disk of light. 

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.