EQUATION OF TANGENT WHICH IS PARALLEL OR PERPENDICULAR TO THE LINE
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
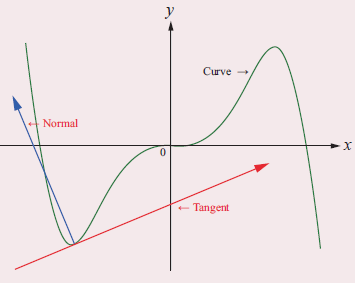
Tangent :
The tangent line (or simply tangent) to a plane curve at a given point is the straight line that just touches the curve at that point.
Equation of tangent :
(y-y1) = m(x-x1)
Normal :
The normal at a point on the curve is the straight line which is perpendicular to the tangent at that point. The tangent and the normal of a curve at a point are illustrated in the adjoining figure.
Equation of normal :
(y-y1) = (-1/m)(x-x1)
Problem 1 :
Find the equations of the tangents to the curve
y = 1+x3
for which the tangent is orthogonal with the line
x+12y = 12
Solution :
y = 1+x3
Slope of tangent drawn at the point (x, y).
dy/dx = 3x2
Slope of normal = -1/3x2 ------(1)
The tangent line is perpendicular to the given line
x+12y = 12
y = -x/12 + 1
Slope (m) = -1/12 ------(2)
(1) = (2)
-1/3x2 = -1/12
3x2 = 12
x2 = 4
x = 2, -2
y = 1+x3
|
When x = 2 y = 1+23 y = 9 |
When x = -2 y = 1+(-2)3 y = -7 |
So, the required points are (2, 9) and (-2, -7)
Equation of tangent :
Slope of tangent at the point (2, 9) is
m = 3(2)2
m = 12
Equation of tangent at the point (2, 9) :
(y-9) = 12(x-2)
y-9 = 12x-24
12x-y-24+9 = 0
12x-y-15 = 0
Equation of tangent at the point (-2, -7) :
(y+7) = 12(x+2)
y+7 = 12x+24
12x-y+24-7 = 0
12x-y+17 = 0
Problem 2 :
Find the equations of the tangents to the curve
y = (x+1)/(x-1)
which are parallel to the line x+2y = 6.
Solution :
y = (x+1)/(x-1)
Differentiating with respect to x.
Using quotient rule,
u = x+1 and v = x-1
u' = 1 and v' = 1
dy/dx = (x-1)(1)-(x+1)(1) / (x-1)2
= (x-1-x-1) / (x-1)2
= -2/(x-1)2 ---(1)
Slope of the given line :
x+2y = 6
y = -x/2+3
m = -1/2---(2)
Since the tangent drawn to the curve at the point (x, y) is parallel to the given line
(1) = (2)
-2/(x-1)2 = -1/2
4 = (x-1)2
(x-1) = ±2
|
x-1 = 2 x = 3 y = (3+1)/(3-1) y = 2 |
x - 1 = -2 x = -1 y = (-1+1)/(-1-1) y = 0 |
Equation of the tangent passes through (3, 2) :
y-2 = (-1/2)(x-3)
2(y-2) = -1(x-3)
2y-4 = -x+3
x+2y-4-3 = 0
x+2y-7 = 0
Equation of the tangent passes through (-1, 0) :
y-0 = (-1/2)(x+1)
2y = -1(x+1)
2y = -x-1
x+2y+1 = 0
Problem 3 :
Find the equation of tangent and normal to the curve given by
x = 7 cos t and y = 2 sin t for all t
at any point on the curve.
Solution :
Slope of tangent :
dx/dt = -7 sin t and dy/dt = 2 cos t
dy/dx = 2 cost/(-7 sin t)
dy/dx = (-2/7) (cost/sin t)
Equation of tangent :
(y-2sin t) = (-2/7) (cost/sin t)(x-7cost)
7sint (y-2sin t) = (-2cost)(x-7cost)
(2cost) x + (7sint)y = 14cos2t + 14sin2t
(2cost) x + (7sint)y = 14(cos2t + sin2t)
(2cost) x + (7sint)y = 14(1)
(2cost) x + (7sint)y = 14
Equation of normal :
(y-2sin t) = (7/2) (sin t/cos t)(x-7cost)
2cost (y-2sin t) = (7sint)(x-7cost)
(2cost)y-4sint cost = (7sint)x - 49sint cost
(7sint)x - (2cost)y - 49sint cost + 4sintcost = 0
(7sint)x - (2cost)y - 45sint cost = 0
Problem 4 :
Find the equation of the tangent to the curve
y = x2 – 2x + 7
which is perpendicular to the line 5y - 15x = 13
Solution :
y = x2 – 2x + 7
Differentiate with respect to x, we get
dy/dx = 2x - 2(1) + 0
dy/dx = 2x - 2
Slope of the given line 5y - 15x = 13
5y = 15x + 13
y = 3x + (13/5)
Slope = 3
Slope of the perpendicular line = -1/3
2x - 2 = -1/3
6x - 6 = -1
6x = -1 + 6
6x = 5
x = 5/6
When x = 5/6, we get y = (5/6)2 – 2(5/6) + 7
= 25/36 - 5/3 + 7
= (25 - 60 + 252)/36
= 217/36
Equation of tangent :
y - 217/36 = -1/3(x - 5/6)
y - 217/36 = -x/3 + 5/18
y = -x/3 + 5/18 + 217/36
y = (-12x + 10 + 217)/36
36y = -12x + 227
12x + 36y = 227
Problem 5 :
Find the equation of the normal to the curve y = x3 +2x +6 which are parallel to the line x + 14y + 4 = 0
Solution :
Normal will be parallel to line x + 14y + 4 = 0
14y = - x - 4
y = (-1/14)x - 2/7
Slope = -1/14
y = x3 +2x +6
dy/dx = 3x2 + 2(1) + 0
slope of tangent = 3x2 + 2
Slope of normal = -1/(3x2 + 2)
-1/(3x2 + 2) = -1/14
3x2 + 2 = 14
3x2 = 12
x2 = 4
x = 2 and x = -2
When x = 2, y = 23 +2(2) +6
y = 18
When x = -2, y = (-2)3 +2(-2) +6
y = -12 + 6
y = -6
So, the required points are (2, 18) and (-2, -6)
Equation of normal :
y - 8 = -1/14 (x - 2)
14y - 112 = -x + 2
x + 14y - 112 - 2 = 0
x + 14y - 114 = 0
Equation of normal :
y + 6 = -1/14 (x + 2)
14y + 84 = -x - 2
x + 14y + 84 + 2 = 0
x + 14y + 86 = 0
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
Digital SAT Math Problems and Solutions (Part - 47)
Mar 05, 26 09:19 PM
Digital SAT Math Problems and Solutions (Part - 47) -
Digital SAT Math Problems and Solutions (Part - 46)
Mar 05, 26 08:37 PM
Digital SAT Math Problems and Solutions (Part - 46) -
Digital SAT Math Problems and Solutions (Part - 45)
Mar 05, 26 08:02 PM
Digital SAT Math Problems and Solutions (Part - 45)