EQUATION OF PERPENDICULAR BISECTOR
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Consider the line AB and its perpendicular bisector CD shown below.
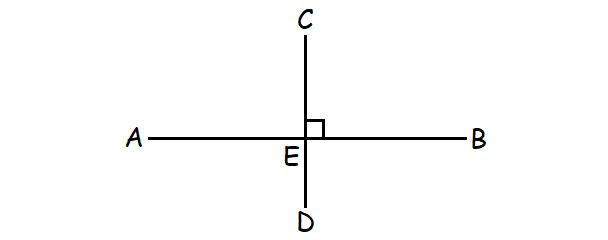
The following steps would be useful to find the equation of the perpendicular bisector CD.
Step 1 :
Find the slope of AB.
Step 2 :
Find the midpoint of AB which is E.
Step 3 :
Since AB and CD are perpendicular,
slope of AB x slope of CD = -1
slope of CD = -1/slope of AB
Step 4 :
Perpendicular bisector CD is passing through the mid point of AB which is E. In slope intercept form equation of a line 'y = mx + b', using the slope of AD and point E, find the y-intercept 'b'.
Step 5 :
Write the equation of perpendicular bisector CD using the slope of CD, 'm' and y-intercept 'b'.
Example 1 :
Find the equation of perpendicular bisector of the line joining the points A(-4, 2) and B(6, -4) in general form.
Solution :
Let E be the mid point and CD be the perpendicular bisector of AB.
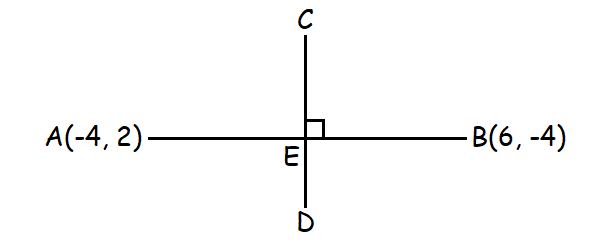
Mid point of AB :
= E((x1 + x2)/2, (y1 + y2)/2)
Substitute (x1, y1) = A(-4, 2) and (x2, y2) = B(6, -4).
= E((-4 + 6)/2, (2 - 4)/2)
= E(2/2, -2/2)
= E(1, -1)
Slope of AB :
= (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = A(-4, 2) and (x2, y2) = B(6, -4).
= (-4 - 2)/(6 + 4)
= -6/10
= -3/5
Slope of AD :
= -1/slope of AB
= -1/(-3/5)
= 5/3
Equation of the perpendicular bisector CD :
y = mx + b
Substitute m = 5/3.
y = (5/3)x + b ----(1)
Substitute (x, y) = E(1, -1).
-1 = (5/3)(1) + b
-1 = 5/3 + b
-1 - 5/3 = b
-8/3 = b
(1)----> y = (5/3)x - 8/3
Multiply each side by 5.
3y = 5x - 8
-5x + 3y + 8 = 0
5x - 3y - 8 = 0
Example 2 :
Write an equation of the line in y = mx + b form that is the perpendicular bisector of the line segment having endpoints of (1, 2) and (2, 4)
Solution :
Let the given points be A(1, 2) and B(2, 4)
Mid point of AB :
= ((x1 + x2)/2, (y1 + y2)/2)
Substitute (x1, y1) = A(1, 2) and (x2, y2) = B(2, 4).
= ((1 + 2)/2, (2 + 4)/2)
= (3/2, 6/2)
= (3/2, 3)
Slope of AB :
= (y2 - y1)/(x2 - x1)
Substitute (x1, y1) = A(1, 2) and (x2, y2) = B(2, 4).
= (4 - 2)/(2 - 1)
= 2/1
= 2
Slope of perpendicular bisector :
= -1/slope of AB
= -1/2
Equation of perpendicular bisector :
y - y1 = m(x - x1)
y - 3 = (-1/2)(x - (3/2))
2(y - 3) = -1(x - 3/2)
4(y - 3) = -1(2x - 3)
4y - 12 = -2x + 3
2x + 4y - 12 - 3 = 0
2x + 4y - 15 = 0
2x + 4y = 15
4y = -2x + 15
y = (-1/2)x + (15/4)
Example 3 :
The straight line p has the equation 3x − 4y + 8 = 0. The straight line q is parallel to p and passes through the point with coordinates (8, 5).
a Find the equation of q in the form y = mx + c. The straight line r is perpendicular to p and passes through the point with coordinates (−4, 6).
b Find the equation of r in the form ax + by + c = 0, where a, b and c are integers.
c Find the coordinates of the point where lines q and r intersect.
Solution :
a) The lines p and q are parallel to each other, then their slopes will be equal.
3x − 4y + 8 = 0
4y = 3x + 8
y = (3/4)x + (8/4)
y = (3/4)x + 2
Slope of the line q = 3/4
Line q is passing through the point (8, 5).
Equation of line q :
y - y1 = m(x - x1)
y - 5 = (3/4)(x - 8)
4(y - 5) = 3(x - 8)
4y - 20 = 3x - 24
3x - 4y - 24 + 20 = 0
3x - 4y = 4 -----(1)
b) Line r is perpendicular to p
Slope of the line r = -1/(3/4)
= -4/3
Line r passes through the point (-4, 6)
y - 6 = (-4/3)(x - (-4))
3(y - 6) = -4(x + 4)
3y - 18 = -4x - 16
4x + 3y - 18 + 16 = 0
4x + 3y = 2 -----(2)
c) 3x - 4y = 4 and 4x + 3y = 2
(1) x 3 ==> 9x - 12y = 12
(2) x 4 ==> 16x + 12y = 8
25x = 20
x = 20/25
x = 4/5
Applying x = 4/5 in (1), we get
3(4/5) - 4y = 4
(12/5) - 4y = 4
4y = (12/5) - 4
4y = -8/5
y = -2/5
So, the point of intersection is (4/5, -2/5)
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations -
10 Hard SAT Math Questions (Part - 4)
Jan 05, 26 06:56 PM
10 Hard SAT Math Questions (Part - 4) -
10 Hard SAT Math Questions (Part - 3)
Jan 05, 26 06:34 PM
10 Hard SAT Math Questions (Part - 3)

