EQUATION OF LINE WORKSHEET
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
1. Find the general equation of a line whose slope is 3 and y-intercept is 4.
2. Find the general equation of a line passing through the point (3, 0) with slope -6.
3. Find the general equation of a line passing through the point (2, 5) with slope -5.
4. Find the general equation of a line passing through the points (-1, 1) and (2, -4).
5. If the x-intercept and y-intercept of a line are 2/3 and 3/4 respectively, find the general equation of the line.
6. Find the equation of a line which is parallel to x-axis and passing through the point (2, 3).
7. Find the general equation of a line which is parallel to the line 3x - 7y = 12 and passing through the point (6, 4).
8. Find the equation of a line which is perpendicular to the line y = (4/3)x - 7 and passing through the point (7, –1).
9. Find the equation of line in slope-intercept form.
10. Cost of producing 10 dolls is $160 and that of 25 dolls is $385. Assuming the cost curve to be linear, find the cost of 50 dolls.

Answers
1. Answer :
Given : slope is 3 and y-intercept is 4.
Equation of a line in slope-intercept form :
y = mx + b
Substitute m = 3 and b = 4.
y = 3x + 4
Subtract y from each side.
0 = 3x - y + 4
3x - y + 4 = 0
2. Answer :
Given : point (3, 0) and slope = -6.
Equation of line in point-slope form :
y - y1 = m(x - x1)
Substitute (x1 , y1) = (3 , 0) and m = -6.
y - 0 = -6(x - 3)
Simplify.
y = -6x + 18
Add 6x to each side.
6x + y = 18
Subtract 18 from each side.
6x + y - 18 = 0
3. Answer :
Given : point (2, 5) and slope = -5.
y = mx + b
Substitute m = -5.
y = -5x + b ----(1)
Substitute (x, y) = (2, 5).
5 = -5(2) + b
Simplify.
5 = -10 + b
Add 10 to each side.
15 = b
Substitute 15 in (1).
(1)----> y = -5x + 15
Add 5x to each side.
5x + y = 15
Subtract 15 from each side.
5x + y - 15 = 0
4. Answer :
Given : Two points on the straight line : (-1, 1) and (2, -4).
Equation of line in two-points form :
(y - y1)/(y2 - y1) = (x - x1)/(x2 - x1)
Substitute (x1 , y1) = (-1, 1) and (x2, y2) = (2, -4).
(y - 1)/(-4 - 1) = (x + 1)/(2 + 1)
Simplify.
(y - 1)/(-5) = (x + 1)/3
Cross multiply.
3(y - 1) = -5(x + 1)
3y - 3 = -5x - 5
5x + 3y + 2 = 0
5. Answer :
Given : x-intercept is 2/3 and y-intercept is 3/4.
Equation of straight line in intercept form :
x/a + y/b = 1
Substitute a = 2/3 and b = 3/4.
x/(2/3) + y/(3/4) = 1
Simplify.
3x/2 + 4y/3 = 1
(9x + 8y)/6 = 1
Multiply each side by 6.
9x + 8y = 6
Subtract 6 from each side.
9x + 8y - 6 = 0
6. Answer :
Given : Required line is parallel to x-axis and passing through the poi point (2, 3).
Equation of line parallel to x-axis :
y = k -----(1)
The line is passing through (2, 3).
So, substitute (x, y) = (2, 3).
3 = k
Substitute k = 3 in (1).
y = 3
7. Answer :
Given : Required line is parallel to 3x - 7y = 12 and passing through the poi point (6, 4).
Equation of line parallel to 3x - 7y = 12 :
3x - 7y + k = 0 -----(1)
The line is passing through (6, 4).
So, substitute (x, y) = (6, 4).
3(6) - 7(4) + k = 0
Simplify.
18 - 28 + k = 0
-10 + k = 0
Add 10 to each side.
k = 10
Substitute k = 10 in (1).
(1)----> 3x - 7y + 10 = 0
8. Answer :
Given : Required line is perpendicular to y = (4/3)x - 7 and passing through the poi point (7, -1).
Write the equation y = (4/3)x - 7 in general form.
y = (4/3)x - 7
Multiply each side by 3.
3y = 4x - 21
Subtract 3y from each side.
0 = 4x - 3y - 21
4x - 3y - 21 = 0
Equation of a line perpendicular to 4x - 3y - 21 = 0.
3x + 4y + k = 0 ----(1)
The line is passing through (7, -1).
So, substitute (x, y) = (7, -1).
3(7) + 4(-1) + k = 0
Simplify.
21 - 4 + k = 0
17 + k = 0
Subtract 17 from each side.
k = -17
Substitute k = -17 in (1).
(1)----> 3x + 4y - 17 = 0
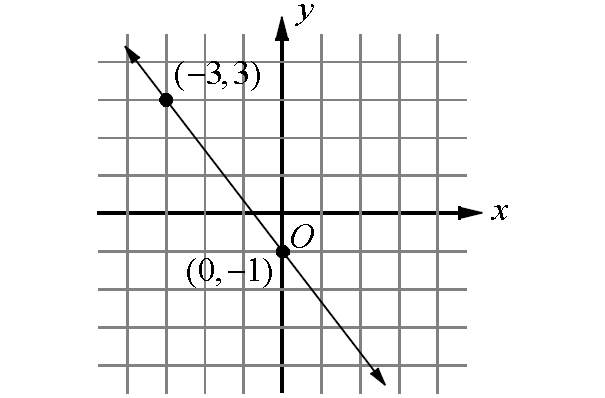
9. Answer :
The given line is a falling line. So, its slope will be a negative value.
Measure the rise and run.
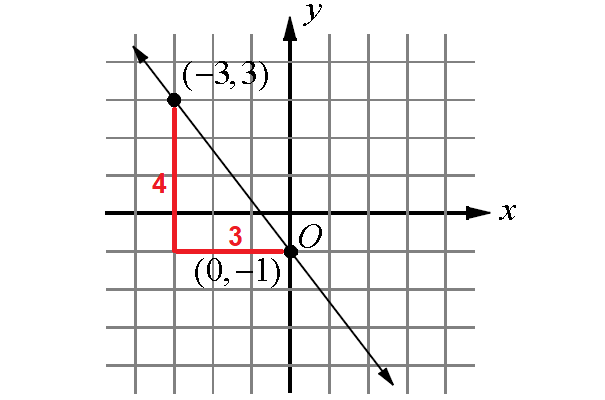
From the above diagram, rise = 4 and run = 3.
slope = rise/run
= -4/3
The line in the diagram above intersects y-axis at -1.
So, y-intercept is -1.
Equation of the line in slope intercept form :
y = mx + b
Substitute m = -4/3 and b = -1.
y = -4x/3 - 1
10. Answer :
Given : Cost of 10 dolls is $160, 25 dolls is $385 and the cost curve is linear.
Since the cost curve is linear, the function which best fits the given information is equation of line in slope-intercept form.
y = Ax + B
y ----> Total cost
x ----> Number of dolls
Target : Find the cost 25 dolls. That is, the value of y when x = 95.
From the given information,
x = 10, y = 160
x = 25, y = 385
Substitute the above values of x and y in y = Ax + B.
160 = 10A + B
385 = 25A + B
Solv for A and B.
A = 15, B = 10
Cost curve :
y = 15x + 10
Substitute x = 50.
y = 15(50) + 10
= 750 + 10
= 760
So, the cost of 50 dolls is $760.
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 45)
Jan 19, 26 06:14 AM
10 Hard SAT Math Questions (Part - 45) -
10 Hard SAT Math Questions (Part - 44)
Jan 12, 26 06:35 AM
10 Hard SAT Math Questions (Part - 44) -
US Common Core K-12 Curricum Algebra Solving Simple Equations
Jan 07, 26 01:53 PM
US Common Core K-12 Curricum Algebra Solving Simple Equations
