EQUATION OF LINE WITH A POINT AND INTERCEPTS
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Example 1 :
Find the equation of the line passing through the point (9, -1) and having its x-intercept thrice and its y-intercept.
Solution :
Let a and b are x and y-intercepts respectively.
x-intercept = 3(y-intercept)
a = 3b
Intercept form equation of a line :
x/a + y/b = 1
Here, a and b are x and y-intercepts respectively.
The required line is passing through the point (9 , -1)
x/a + y/b = 1
9/3b - 1/b = 1
(9 - 3)/3b = 1
6/3b = 1
2/b = 1
2 = b
y-intercept (b) = 2
x -intercept (a) = 3(2) = 6
x/6 + y/2 = 1
x/6 + 3y/6 = 1
x + 3y = 6
x + 3y - 6 = 0
Example 2 :
A straight line cuts coordinate axes at A and B. If the midpoint of AB is (3, 2), then find the equation of AB.
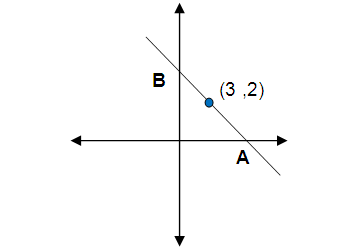
Solution :
x-intercept = a and y-intercept = b
From the picture, coordinates of A are (a, 0) and coordinates of B are (0, b).
Midpoint of AB = (x1 + x2)/2 , (y1 + y2)/2
(3, 2) = (a + 0)/2, (0 + b)/2
By equating x and y coordinates, we get
3 = a/2 2 = b/2
a = 6 b = 4
Intercept form equation of a line :
x/a + y/b = 1
x/6 + y/4 = 1
(2x + 3y)/12 = 1
2x + 3y = 12
2x + 3y - 12 = 0
Example 3 :
Find the equation of the line passing through (22, -6) and having intercept on x-axis exceeds the intercept on y-axis by 5.
Solution :
Let x -intercept be a and y-intercept be b.
x -intercept (a) = b + 5
Intercept form equation of a line :
x/a + y/b = 1
(22/(b+5)) + (-6/b) = 1
[22b - 6(b + 5)]/b(b + 5) = 1
(22b - 6b - 30)/(b2 + 5b) = 1
(16b - 30)/(b2 + 5b) = 1
16b - 30 = b2 + 5b
b2 + 5b - 16b - 30 = 0
b2 - 11b - 30 = 0
(b - 6)(b - 5) = 0
b = 6 or b = 5
|
When b = 6, a = 6 + 5 a = 11 |
When b = 5, a = 5 + 5 a = 10 |
Equation of the line when a = 11 and b = 6 :
x/11 + y/6 = 1
6x + 11y = 66
6x + 11y - 66 = 0
Equation of the line when a = 10 and b = 5 :
x/10 + y/5 = 1
x + 2y = 10
x + 2y - 10 = 0
Equation of the required line is
x + 2y - 10 = 0 or 6x + 11y - 66 = 0
Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
About Us | Contact Us | Privacy Policy
©All rights reserved. onlinemath4all.com

Recent Articles
-
10 Hard SAT Math Questions (Part - 41)
Dec 24, 25 07:58 PM
10 Hard SAT Math Questions (Part - 41) -
ASTC Formula in Trigonometry
Dec 23, 25 11:34 PM
ASTC Formula in Trigonometry - Concepts - Examples and Solved Problems -
Coin Tossing Probability
Dec 23, 25 11:29 PM
Coin Tossing Probability - Concept - Sample Space - Formula - Solved Problems

